The windowless room would have been infinitely black, except for a bright emerald rod of laser light twenty feet from where the door shut out the world behind me. "Come this way," beckoned one of the experimenters. Taking my arm like an usher at a seance, he led me to a stool opposite the laser gun. "Don't look directly into the beam," his partner warned, unnecessarily. The usher slipped a photographic plate into a frame in the beam's path. Instantly, a dissected human brain appeared in the space before me.
It was one of my own specimens, from my class demonstration collection. I'd made the dissection with great care the previous year and had loaned it to the experimenters a few weeks before. But I knew for certain that this specimen was now across the hallway, safely stored in a pickle jar and locked in a cabinet whose only key was in my pants pocket. Yet as an optical phenomenon the specimen was right here in the room with the three of us.
I had known what would be in the room. At least I'd thought I knew. I understood the technical side of what was happening, as did my students. Yet I found myself wondering, as they must have, just what "real" really means. Visually, I could make no distinction between what I was seeing and the actual object. I looked down into a complexly shadowed recess of the specimen where I'd dissected away the forward part of the temporal lobe and had pared back the cerebrum to expose the optic tract and LGB; and I saw features not even the best stereoscopic photographs can capture. When I shifted my gaze to the right, structures I hadn't seen over on the left came instantly into view. When I stood and looked down, I could see the top of the specimen. As I backed off, more structures filled my visual field, and their individual details became less distinct. As I moved in close, fewer structures occupied my field of view, but those that were there I saw much more clearly. Moving still closer, I made out gridlike indentations gauze had pressed into the soft cerebral cortex before the brain had been transferred to formaldehyde and had hardened. And I suddenly became aware that, from habit, I was holding my breath, anticipating a whiff of strong formaldehyde fumes. Finally, even though the scientist in me knew better, I was compelled to reach out and try to touch the brain, to convince myself the object wasn't there.
My students and I weren't hallucinating, observing trick photography, experiencing illusions, or skirting the edges of the occult. In the strictest technical sense we had been looking at the actual brain, even though it wasn't there. We had witnessed the decoding of an optical hologram.
***
How does a forest or a stained- glass window communicate a visible presence? How do objects let us see them? How do they impress their features onto light?
Physical theory tells us that light, emitted and absorbed as photons-- as particles--travels as waves, waves of mass-energy. Light is mass-energy in extreme motion (if Einstein was right). Except for the fleeting instant when mass-energy becomes light, or ceases to be light, it is waves. Objects change waves; they warp them. The warp is the optical message, and its specific character depends first of all on what the waves were like just before they illuminated the scene, and, second, on the nature of the objects. If the object indiscriminately absorbs waves of energy, as for example a patch of tar does, its image will appear to us to be dark, because very little light radiates away from it and into the optical environment. If the object has little capacity to absorb energy, as is the case with the fur of an albino mink, say, then light will be warped by contours and edges, but the image will appear white in white light, blue in blue light, red in red light, and so forth. If the object absorbs particular colors or wavelengths, it will subtract those energies from a mixture and will reflect or transmit the rest. White light, which is a mixture of the colors of the rainbow, contains the waves for an infinite variety of hues. The primary colors red, green, and blue, can combine to form the 500,000 or more hues a human eye can discriminate.[1] In addition, objects distort the waves relative to the sharpness, smoothness, or complexity of their contours. But the totality of the optical message travels in the form of a warp.
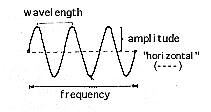
In all electromagnetic radiation, including light, the shorter the wavelength the greater the energy. Offhand, this may seem wrong. But think of the pleats of an accordion. Compressing the bellows, thereby forcing the pleats together, concentrates the train of wavelets and increases their number per inch. In electromagnetic radiation, likewise, the shorter the wavelength, the greater the frequency , or number of wavelets per second. Also, as wavelength decreases, the amplitude of each wavelet increases: the peaks become taller, the troughs deeper. You might say that compressed waves become more "ample." Physicists define amplitude as the maximum rise of the wave's crest from the horizontal surface, from the midpoint between peak and trough. The intensity of light is proportional to the amplitude, or the crest height.
According to Einstein, mass-energy has reached the maximum attainable velocity when it assumes the form of light. Conversely, when mass-energy hasn't reached that maximum speed, it isn't light. Energy is more concentrated in blue light than in, say, red light. Since the mass-energy can't move any faster or slower, and since something must accommodate the difference, blue light waves compress closer together than red ones; and, compared to red waves, blue waves exhibit greater amplitude and frequencies, and shorter wavelengths.
But not all waves move at the speed of light. Water waves certainly don't, nor do sound waves. Unlike light, the amplitude and frequency of these waves are independent of each other. This is why for example, a high-pitched squeak may be of very low amplitude, and a deep, rumbling, low-frequency bass sound may be intense enough to knock you out of your seat.
But one thing is true about any wave: put amplitude together with phase and you completely define the wave. As mathematical physicist Edgar Kraut has written, "A complete knowledge of the amplitude and phase spectra of a function [the mathematical essentials of an equation] determines the function completely."[2] Kraut uses the term spectra because phase and amplitude define not only simple waves but complex ones as well. We'll see later in the book that complex waves are made up of simple, regular waves.
What is wave phase? The formal definition of the term describes it as that part of a cycle a wave has passed through at any given instant. Engineers and physicists use the term cycle almost interchangeably with wavelet . This is because the points on a simple, regular wavelet relate directly to the circumference of a circle, or a cycle. For example, if what is known as a sine wavelet has reached its amplitude, it has passed the equivalence of ninety degrees on the circle.
 ----->
----->
 ....
....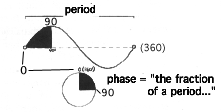
Phase, as I have said, is a sizeless entity -- sizeless in the sense that we can't measure it with a yardstick or weigh it on a scale. We speak of phase in terms of angles or their equivalents, or in terms of time. And to create an angle, or to specify it, we need more than a single entity. Phase demands a reference, something to compare it with. Because phase is relative, we cannot treat it, or even conceptualize it, as an absolute.
We can appreciate both the nature of phase and the problems in dealing with it by looking at the face of a clock. The revolutions of the hands around the dial describe the phase of the hour of the AM or PM. The hands move at different rates and exhibit different phases. Yet the phase difference--the relative phase--converts the seemingly abstract, invisible, untouchable, ever-beginning, never-ending dimension, time, into our time--people time! Five-thirty is the phase of the morning when we must crawl out of the sleeping bag and milk the goat. Four-fifteen is the phase of the afternoon when children will be getting off the school bus expecting warm cookies and cold orange juice. Phase on the clock has the same theoretical meaning as it does on a wavy surface. Thus relative wave phase is a part of our everyday lives.
***
In an optical hologram, such as the one my students and I experienced, the encoded message exists in a special kind of shadow, the interference pattern--alternating zones of light and dark. The densities of the shadows depend on the intensity of the light, and carry the information about amplitude. How rapidly the shadows change from light to dark depends on relative phase, and thus carries the phase code. As I mentioned earlier, objects warp light; they warp amplitude and phase. The warp, in turn, creates the shadows. In fact, the shadows are transformations of the wave's phase and amplitude warps to a kind of mathematical warp in the photographic plate. When the correct decoding beam passes through those shadows, the shadows warp beam's waves. The shadows force into the decoding beam the very phase and amplitude changes that created them in the first place. And when the decoding beam forms an image, it is, by every physical standard, completely regenerating the scene as an optical phenomenon, even though the objects may be gone.
What about photographs? They, and all conventional pictures, capture intensities of light from a scene. Photographs encode information about amplitude but not phase.
***
Optical holograms encode for amplitude as well as for phase variations in the scene. The basic reason for this has to do with the nature of light, with the waves' attainment of maximum speed. But other kinds of waves also make holograms. An acoustical holographer, Alexander Metherell, some years ago had a hunch that phase was really the generic essence of the hologram. Of course we can't have phase all by itself, except in the abstract, which Metherell , of course knew. But he wondered if he might assume just one amplitude--create a constant background din--and then encode the message strictly with phase variations. It worked. And Metherell went on the demonstrate his point with the phase-only holograms I referred to earlier.
I mention phase-only holograms at this juncture to make a point about hologramic mind. The frequencies and energy levels in the nervous system do not remotely approach those of light. For this reason, we can't make a literal comparison between optical and neural holograms, at least not in using hologramic theory. Also, because of phase-only holograms, amplitude variations would not play a necessary and indispensable role in the storage of information in the brain. Phase is the essence of hologramic mind!
Before I supply more background on holograms, per se, let me raise still another important preliminary question. What do we actually mean when we use the word wave ? Let's take an introspective look.
***
Many of us first became acquainted with the word wave when someone hoisted us from the crib or playpen, gently kissed us on the side of the head, and coaxed, "Wave bye-bye to Uncle Hoibie!" Later, we may have thought "wave" as we pressed a nose against the cool windowpane and watched little brother Ben's diapers waving on the clothesline in the autumn breeze. Then one Fourth of July or Saint Patrick's Day, our mother perhaps gave us a whole quarter; we ran to the candy store on the corner, and, instead of baseball cards and bubble gum, we bought a little American flag on a stick. We ran over to the park and waved the little flag to the rhythm of the march; then we began to laugh our heads off when the mounted policemen jiggled by in their saddles, out of time with each other and the beat of the drums and the cadence we were keeping with the little waving flag. Still later, perhaps, we learned to wave Morse code with a wigwag flag, dot to the right, dash to the left. Up early to go fishing, when radio station W-whatever-the-heck-it-was signed on, we may have wondered what "kilocycles" or "megahertz" meant. And it was not until after we began playing rock flute with the Seventh Court that the bearded electronic piano player with the Ph.D. in astronomy said that "cycle" to an engineer is "wavelet" to a sailor, and that the hertz value means cycles per second--in other words, frequency. If we enrolled in physics in high school, we probably carried out experiments with pendulums and tuning forks. An oscillating pendulum scribed a wave on a smoked, revolving drum. A vibrating tuning fork also created waves, but of higher frequency: 256 cycles per second when we used the fork with the pitch of middle C on the piano. Moving down an octave, according to the textbook, would give us 128 hertz.
Are our usages of wave metaphorical? The word metaphor has become overworked in our times. While I certainly wouldn't want to deny waves to poets, I don't think metaphor is at the nexus of our everyday usage of wave . Analog is a better choice: something embodying a principle or a logic that we find in something else. (Notice the stem of analog.)
To and fro, rise and fall, up and down, over and under, in and out, tick and tock, round and round, and so on... Cycles. Periodicities. Recurrences. Undulations. Corrugations. Oscillations. Vibrations. Round-trip excursions along a continuum, like the rise, fall, and return of the contour of a wavelet, the revolutions of a wheel, the journey of a piston, the hands of a clock. These are all analogs of waves.
Do we really mean that pendular motion is a symbolic expression of the rotations of a clock's hands? No. The motion of one translates into continuous displacements of the other. Is the ride on a roller coaster an allegorical reference to the course of the tracks? Of course not. The conduct of the one issues directly from the character of the other, to borrow a phrase from a John Dewey title. And why would we suppose that a pendulum or a tuning fork could scribe a wave? The answer is that the same logic prevails in all periodic events, patterns, circumstances, conditions, motions, surfaces, and so forth.
No, a child's hand isn't the same thing as a fluttering piece of cloth or the ripples on a pond. And yes, there's imprecision and imperfection in our verbal meanings; we wouldn't want it otherwise. Poetry may exist in all of this. Yet by our literal usages of wave we denote what Plato would have called the idea of waviness, the universal logic revealed by all things wavy. And that logic translates, completely, into amplitude and phase. And if the medium stores phase information, we have a species of hologram.
***
Not all physics is about waves, of course. The liveliest endeavor in that science today, the pursuit of the quark, is a search for fundamental particles -- discrete entities -- of mass-energy. The photon is a light particle. Light is both particles and waves. The same is true of all mass-energy at the atomic level. The electron microscope, for example, depends on electrons, not as the particles we usually consider them to be but as the electron waves uncovered in the 1920s as the result of de Broglie's theories. And one of the tenets of contemporary physics is that mass-energy is both particulate and wavy. But when we are dealing with particles, the wavy side of mass-energy disappears; and when it is measured as waves, mass-energy doesn't appear as particles. If you want to concentrate on corpuscles of light, or photons, you must witness the transduction of a filament's mass-energy into light, or from light into some other form, as occurs in the quantized chemical reactions in our visual pigment molecules. But if the choice is light on the move between emission and absorption, the techniques must be suitable for waves.
Physics would be a side show in our times if the logic of waves had been left out of science. And waves might have been left out of science, were it not for Galileo's discovery of the rules of the pendulum. The pendulum taught us how to build accurate clocks. Without a reliable clock, astronomy would be out of the question. And how could anybody contemplate timing something such as the speed of light without a good clock? It was in 1656 that a twenty-seven-year-old Dutchman named Christian Huygens invented the pendular clock.
Huygens wasn't just a back-room tinkerer. His work with the pendulum was the result of his preoccupation with waves. The reader may recognize Huygens's name from his famous wave principle. He had studied the question of how waves spread to make an advancing wave front. Have you ever observed ripples diverging in ever-expanding circles from the point where you drop a rock into the water? If not, fill a wash basin halfway, and then let the faucet drip...drip...drip! Huygens explained how one set of ripples gives rise to the next. He postulated that each point in a ripple acts just like the original disturbance, creating tiny new waves. The new waves than expand and combine to make the next line of ripples, the advancing wave front. A diagram in a treatise Huygens published in 1690 is still the prototype for illustrations of his principle in today's physics textbooks.
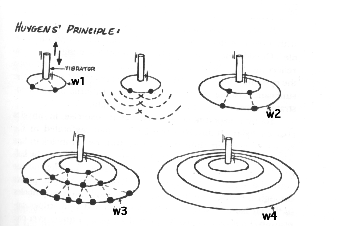
We can't see light waves. Even today, the light wave is a theoretical entity. And to scholars in Huygen's times, nothing seemed sillier or more remote from reality than light waves.
But on November 24, 1803, Thomas Young, M.D.., F.R.S., thought it right "to lay before the Royal Society a short statement of the facts which appear so decisive to me..."
"I made a small hole in a window-shutter, and covered it with a piece of thick paper, which I perforated with a fine needle." [sniff!] Outside the shutter "I placed a small looking-glass...to reflect the sun's light, in a direction nearly horizontal, and upon the opposite wall." And with perforated cards in the path of "the sunbeam," Young produced interference patterns and demonstrated, conclusively, the wavy nature of light.

Interference patterns guarantee waves. But Young's work wasn't immediately accepted by British scientists. In fact, if he had not been active in many other fields (the range of his intellect is astonishing), he might never have been allowed to lay another thing before the Royal Society. Young's critics, according to his biographer, George Peacock, "diverted public attention from examination of the truth."[4]
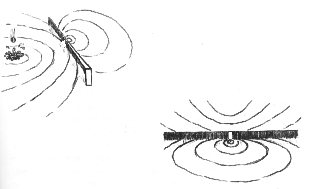
It wasn't Arago's original research that vindicated and extended Young's theory, however, but that of Augustin Jean Fresnel, with whom Arago collaborated.
Fresnel! When my mind says "Fray-nel!" in poor Ph.D. language-examination French, certain words of Charles Peirce also surface: "These are men whom we see possessed by a passion to learn...Those are the naturally scientific men."[5] Fresnel's work brought him little renown in his lifetime. But optical physicists today use his name as an adjective. For Fresnel demonstrated just what interference is all about.
Interference occurs whenever waves collide. You've probably seen waves of water cancel each other upon impact. This is destructive interference, which occurs when the rising part of one wave meets the falling part of another. Conceptually, destructive interference is like adding a positive number to a negative number. On the other hand, when waves meet as both are moving up together, interference still occurs but it is constructive , or additive, and the resulting wave crests higher than its parents. In order to have an interference pattern, some definite phase relationship must exist between two sets of colliding waves. A well-defined phase relationship is coherent and is often referred to as "in step". When colliding waves are incoherent, their interaction produces random effects. An interference pattern is not random; and a basic requirement in an interference pattern is coherency.
Ordinary light is decidedly incoherent, which is why optical interference patterns aren't an everyday observation. Today, Heisenberg's uncertainty principle[6] accounts for this: wicks and filaments emit light in random bursts. Even if we filter light waves -- screen out all but those of the same amplitude, wavelength, and frequency -- we can't put them in step. In other words, we can't generate a definite phase relationship in light waves from two or more sources.
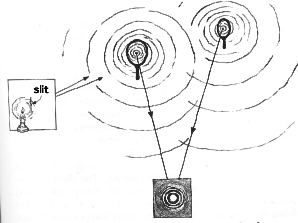
Young's experiment circumvented the uncertainty principle in a remarkably simple way. Recall that his sunbeam first passed through a single pinhole. Therefore, the light that went through both pinholes in the far baffle, having come from the same point source, and being the same light, had the same phase spectrum. And, coming out of the other side of the far baffle, the two new sets of waves had a well-defined phase relationship, and therefore the coherency to make interference fringes.
Here's what Fresnel did. He let light shine through a slit. Then he lined up two mirrors with the beam, aiming them so as to reflect light toward a screen. But he set the two mirrors at unequal distances from the screen. In so doing, he introduced a phase difference between the waves reflected by each mirror. But because the waves came from the same source (the slit), their phase differences were orderly; they were coherent. And when they interfered, they produced fringes in the form of Fresnel rings.
Interference patterns not only depend on an orderly phase difference, they are precisely determined by that difference. If you are ever in a mood to carry out Young's experiment, see what happens when you change the distance between the two holes (create a phase variation, in other words). You'll find that the closer the openings, the narrower the fringes (or beats) will be and the greater the number of fringes on the screen.
***
The hologram was born in London on Easter Sunday morning, 1947. It was just a thought that day, an abstract idea that suddenly came alive in the imagination of a Hungarian refugee, the late Dennis Gabor. The invention itself, the first deliberately constructed hologram, came a little later. But even after Gabor published his experiments in the British journal Nature the following year, the hologram remained virtually unknown for a decade and a half. Gabor's rudimentary holograms had none of the dramatic qualities of holograms today; perhaps as few as two dozen people, worldwide, appreciated their profound implications. Not until 1971, after holography had blossomed into a whole new branch of optics, did Gabor finally receive the Nobel Prize.
Gabor often related his thinking on that fateful Easter morning. He hadn't set out to invent the hologram. His thoughts were on the electron microscope, then a crude and imperfect device. In theory, the electron microscope should have been able to resolve atoms.[7] (Indeed, some instruments do today.) But in 1947, theory was a long way from practice. "Why not take a bad electron picture." Gabor recounted in his Nobel lecture, "but one which contains the whole of the information, and correct it by optical means?"[8]
The entire idea hinged on phase. And Gabor solved the phase problem with the conceptual approach Albert Einstein had taken in theorizing mass-energy and, eventually, the universe itself. No wonder we lose the phase, Gabor thought, if there is nothing to compare it with! He would need a reference . He would have to deal with phase information in relative, not absolute, terms.
The big technical hurdle was coherency. How could he produce a coherent source? Gabor's answer was very similar in principle to Young's and Fresnel's: Let light shine through a pinhole. If he set a tiny transparent object in the path of the beam, some waves--object waves--would pass through it, while others would miss; the waves that missed the object would still collide with the object waves downstream, and that ought to create interference patterns. Those waves that missed the object would become his reference. And the interference patterns would become a record of the phase and amplitude differences between object and reference waves. He'd use a photographic plate to capture that pattern, he decided.
Recall the discussion about objects warping the amplitude and phase of waves? If the interference pattern is completely determined by the amplitude and phase spectra of interacting sets of waves, then what? The hologram should retain not only amplitude changes but also the relative phase variations imposed on the object waves.
It is hard to believe that such records had already been produced by other physicists. But as a matter of fact, x-ray crystallographers' diffraction patterns, generically speaking, are holograms. Crystallographers take the information from the x-ray diffraction patterns and use the equations Kraut was talking about to deduce the images of the atoms in crystals. Gabor realized that he could do the same thing with a beam of light. He could physically decode the image. He realized that if he passed the original light through the hologram plate, instead of through the object, the shadows in the hologram would put the warp into those waves and the complete image would appear where the object had been. For this would reconstruct the image-bearing wave front. When he tried it, it worked.
***
The object Gabor used for his very first hologram was a tiny transparent disc with a microscopic but monumental message etched onto it. It read, "Huygens, Young, Fresnel."
Gabor did not succeed with the electron microscope. In fact, his first hologram just barely reconstructed the message. "It was far from perfect," he quipped. But it was not his reconstruction that had made history. It was the idea.
***
Gabor's principle is very simple, in retrospect--so simple that only a genius could have seen through the taboos of the time to find the hologram amid the arcane and abstract properties of waves.
The hologram is an interference pattern, and interference is a subject taught in high school physics courses. To engineers and physicists, the hologram is a straightforward extension of elementary optics. Even the mathematics of the hologram are fairly simple. Crystallographers for some time had been doing the construction step of holography without calling it that. And a color technique developed in 1894 (the Lippman process) suggested even the reconstruction step. How then was it possible for the hologram to escape modern science until 1947?
Science is people. Scientists seldom try out in their laboratories what they do not believe in their guts. Recording the phase of light waves would violate the uncertainty principle. Nothing yet known has withstood the incredible power of the uncertainty principle, including the hologram. There's a subtle distinction, though, between phase and a code resulting from phase. But only an extraordinary mind could see this; and only an extraordinary person had the courage to proceed from there.
Gabor was no ordinary person. And in the early 1960s. in Michigan, two other extraordinary persons entered the scene--Emmett Leith and Juris Upatnieks. A small amount of work had been done in this field after Gabor's research; but Leith and Upatnieks turned Gabor's rudimentary discovery into holography as it is practiced today. And among their long string of remarkable inventions and discoveries was one that precipitated nothing less than hologramic memory theory itself.
***
The germ of hologramic memory is unmistakable in Gabor's original discoveries--in retrospect. A physicist named van Heerden actually proposed an optical theory of memory in 1963; but his work went as unnoticed as Gabor's had. As in the case of the acorn and the oak, it is difficult to see the connection, a priori. Leith and Upatnieks did for the hologram what Gabor had done for interference in general: they extended it to its fullest dimensions.
Leith had worked on sophisticated radar, was a mathematical thinker, and thoroughly understood waves; and in 1955 he had become intrigued by the hologram. Upatnieks was a bench wizard, the kind of person who when you let him loose in a laboratory makes the impossible experiment work.
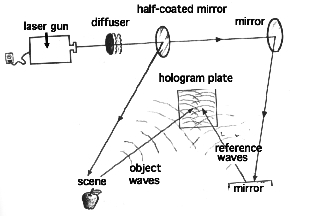
Gabor's so-called "in-line" method (because object lies between plate and source) put several restrictions on optical holograms. For instance, the object had to be transparent. This posed the problem of what to do about dense objects. Besides, we actually see most things in reflected light. Leith and Upatnieks applied an elaborate version of Fresnel's old trick: they used mirrors. Mirrors allowed them to invent "off-line" holograms, and to use reflected light. The light came from a point source. The beam passed through a special partially coated mirror, which produced two beams from the original; and other mirrors deflected the two beams along different paths. One beam, aimed at the object, supplied the object waves. The other beam furnished the reference waves. They by-passed the scene but intersected and interfered with the reflected object waves at the hologram plate.
Leith and Upatnieks used a narrow beam from an arc lamp to make their early holograms. But there was a problem. The holographed scene was still very small. To make holograms interesting, they needed a broad, diffuse light. But with ordinary light, a broad beam wouldn't be coherent.
So Leith and Upatnieks turned to the laser. The laser had been invented in 1960, shortly before Leith and Upatnieks tooled up to work on holograms. The laser is a source of extremely coherent light, not because it disobeys the uncertainty principle but because each burst of light involves a twin emission--two wave trains of identical phase and amplitude.
***
Gabor had tried to make his object act like a single point source. The encoded message spread out over the medium. But each point in the scene illuminated by diffuse light acts as though it is a source in itself; and the consequence of all points acting as light sources is truly startling. Each point in the hologram plate ends up with the phase and amplitude warp of every point in the scene, which is the same as saying that every part of the exposed plate contains a complete record of the entire object. This may sound preposterous. Therefore, let me repeat: Each point within a diffuse hologram bears a complete code for the entire scene. If that seems strange, consider something else Leith and Upatneiks found: "The plate can be broken down into small fragments, and each piece will reconstruct the entire object."[9]
How can this be? We'll have to defer the complete answer until later. But recall the sizeless nature of relative phase, of angles and degrees. The uncanny character of the diffuse hologram follows from the relative nature of phase information. In theory, a hologram's codes may be of any size, ranging from the proportions of a geometric point up to the magnitude of the entire universe.[10]
Leith and Upatnieks found that as fragments of holograms became small, "resolution is, of course, lost, since the hologram constitutes the limiting aperture of the imaging process."[11] They were saying that tiny pieces of a hologram will only accommodate a narrow beam of decoding light. As any signal carrier becomes very tiny, and thus very weak, "noise" erodes the image. But vibrations, chatter, static, snow--noise--have to do with the carrier, not the stored message, which is total at every point in the diffuse hologram. Even the blurred image, reconstructed from the tiny chip, is still an image of the whole scene.
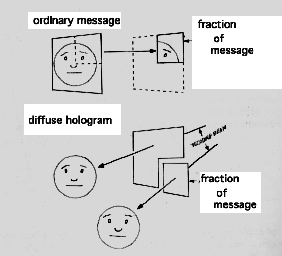
Leith and Upatnieks published an account of the diffuse hologram in the November 1964 issue of the Journal of the Optical Society of America. The following spring, ink scarcely dry on the journal pages, Bela Julesz and K. S. Pennington explicitly proposed that memory in the living brain maps like information in the diffuse hologram. Hologramic theory had made a formal entry into scientific discourse.
***
Whom should we credit then for the idea of the hologramic mind? Lashley? He had forecast it in pointing to interference patterns. Van Heerden? He saw the connection. Pribram? The idea might not have made it into biology without his daring. The cyberneticist Philip Westlake, who wrote a doctoral dissertation to show that electrophysiological data fit the equations of holograms? Julesz and Pennington, for the courage to come right out and say so? I've spent many years unsuccessfully trying to decide just who and when. And I'm not really the person to say. But I am thoroughly convinced of this: subtract Leith and Upatnieks from the scene, and a thousand years could have slipped by with only an occasional van Heerden observing, unnoticed, how closely the hologram mimics the living brain. For the genesis of the theory recapitulates virtually the history of human thought: only after Pythagoras's earth became Columbus's world did it become perfectly obvious to everyone else that our planet was a sphere. And only after Gabor's principle became Leith and Upatnieks's diffuse hologram did science enter the age of the hologramic mind.
Internet contact:pietsch@indiana.edu