What is mathematics, anyway? The American philosopher Charles Peirce, who gave contemporary science its philosophical backbone, observed, "The common definition ...is that mathematics is the science of quantity.[1] But, citing his own mathematician father, Benjamin Peirce, Charles went on to assert that it is actually "The science which draws necessary conclusions." Thus the numbers are not what make a mathematical statement our of 1 + 1 = 2; rather, it's the necessary conclusion forced from 1 and 1 by the plus sign. If we extrapolate Peirce's characterization to our own quest, the payoff ought to be a clear understanding not only of what we mean by "hologramic mind" but also of why hologramic mind does what it does when it does it.
The reader probably can think of many specific examples, though, in which adding one thing to another does not necessarily yield two (even when we keep apples and oranges straight). With scrambled eggs, for example, combining two beaten yolks produces one entity. Bertrand Russell helps us with problems like this, and in so doing furnishes us with an essential caveat: "The problem arises through the fact that such knowledge [mathematical ideas] is general, whereas all experience [egg yolks or salamander brains] is particular.[2]
Our search will uncover hologramic mind not as a particular thing but as a generalization. We will begin the quest in this chapter with a theoretical look at waves. And we will continue our search through the next two chapters. It is important to know in advance that our objective will not be the geography, but the geometry of the mind. Ready? "And a one-y and a two-ey..." as my children's violin teacher used to say.
***
The central idea for our examination of waves originated in the work of an eighteenth-century Frenchman, Pierre Simon, Marquis de Laplace. But it was a countryman of Laplace who in 1822 explicitly articulated the theory of waves we will call upon directly. His name was Jean Baptiste Joseph, Baron de Fourier.
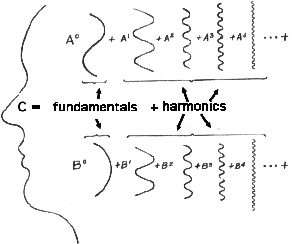
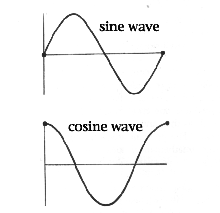
In chapter 3, I mentioned that in theory a compound irregular wave is the coalesced product of a series of simple regular waves. The latter idea is the essence of Fourier's illustrious theorem.[3] The outline of a human face, for example, can be represented by a series of highly regular waves called sine waves and cosine waves.
We're not just talking about waves, however. As, J. W. Mellor wrote in his classic textbook, Higher Mathematics, "Any physical property--density, pressure, velocity--which varies periodically with time and whose magnitude or intensity can be measured, may be represented by Fourier's series."[4] Therefore, let's take advantage of Fourier's theory, and, to assists our imagery, let's think of a compound irregular wave as a series of smaller and smaller cycles ; or better, as wheels spinning on the same axle; or perhaps even better still, as the dials on an old-fashioned gas or electric meter. Waves, after all, are cycles. And wheels and are circles. Now imagine our series with the largest wheel--or slowest dial--as the first in line, and the smallest or fastest back at the tail end of the line. The intermediate wheels progress from larger to smaller, or slower to faster. Or the faster the dial, the more cycles it will execute in, say, a second. In other words, as we progress along the series, frequency (spins or cycles per second) increases as the cycles get smaller.
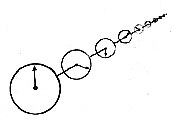
If we were to transform our cycles back to wavy waves, we would see more and more wavelets as we progressed along the series. In fact, in a Fourier series, the frequencies go up--1, 2, 3, 4, 5, 6... and so on.
But wait! If the frequencies of your face and mine go up 1, 2, 3, 4, 5, 6...how can our profiles be different? What Fourier did was calculate a factor that would make the first regular wave a single cycle that extended over the period of the compound wave. Then he calculated factors, or coefficients, for each component cycle--values that make their frequencies 1, 2, 3, 4, 5, 6... or more times the frequency of the first cycle. The individual identities of our profiles, yours and mine, depend on these Fourier coefficients. The analyst uses integral calculus[5] to determine them. Fourier analysis (what else!) is the name applied to the analytical process. Once all the coefficients are available, the analyst can represent the compound wave as a Fourier series. Then the analyst can graph and plot, say, amplitude versus frequency. A graph can be represented by an equation. And an equation using Fourier coefficients to represent a compound wave's amplitude versus frequency is called a Fourier transform, which we'll discuss in the next chapter.
But wait! Isn't there something fish about coefficients? Isn't Fourier analysis like making the compound wave equal ten, for instance, and then saying 10 = 1+2+3+4? If the components don't come out just right, we'll just multiply them by the correct amount to make sure the series adds up to the sum we want. Mellor even quotes the celebrated German physician and physicist, Ludwig von Helmholtz as calling Fourier's theorem "mathematical fiction."[6] But this opinion did not stop Helmholtz and many in his day from using Fourier's theorem. Fourier's ideas gave new meaning to theoretical and applied mathematics long before the underlying conditions had been set forth and the proofs established. Why would anyone in his or her right mind use an unproved formula that had shady philosophical implications? The answer is very human. It worked!
An extremely complicated wave may be the product of many component waves. How many? An infinite number, in theory. How, then, does the analyst know when to stop analyzing? The answer suggests another powerful use of Fourier theorem. The analyst synthesizes the components, step by step--puts them back together to make a compound wave. And when the synthesized wave matches the original profile, the analyst knows it's time to quit adding back components. What would you suppose this synthesis is called? Fourier synthesis, what else! Now when Fourier synthesis produces a wave like the original, the analyst knows he or she has the coefficients necessary to calculate the desired Fourier transform; that is, the equation of the compound wave.
Conceptually, Fourier synthesis is a lot like the decoding of a hologram. But before we can talk about this process, we must know more about the hologram itself. And before that, we must dig deeper still into the theoretical essence of waviness.
***
The first regular wave in a Fourier series is often called the fundamental frequency or, alternatively, the first harmonic. The subsequent waves, the sine and cosine waves, represent the second, third, fourth, fifth, sixth... harmonics. Computer programs exist that will calculate higher and higher harmonics. In the pre-microchip days, nine was considered the magic number; even today, nine harmonics is enough to approximate compound waves with very large numbers of components. As the analysis proceeds, the discrepancy between the synthesized wave and the original wave usually becomes so small as to be insignificant.
These terms may seem very musical to the reader. Indeed, harmonic analysis is one of the many uses of Fourier's theorem. Take a sound from a musical instrument, for example. The first component represents the fundamental frequency, the main pitch of the sound. Higher harmonics represent overtones. There are odd and even harmonics, and they correspond to sine and cosine waves in the series. I present these terms from harmonic analysis only to illustrate one use of Fourier's theorem. But the theorem has such wide application that it has become a veritable lingua franca among persons who deal with periodic patterns, motions, surfaces, events...and on and on. I see no particular reason why the reader should dwell on terms like "fundamentals" and "odd-and-even harmonics." But for our purposes, it is highly instructive to look into why the component waves of Fourier series bear the adjectives, "sine" and "cosine."[7]
The trigonometrist uses sines and cosines as functions of angles,
"function" meaning something whose value depends on something else. A function
changes with variations in whatever determines it. Belly fat changes as a
function of too many peanut-butter cookies changes location from plate to
mouth. Sines and cosines are numerical values that change from 0 to 1 or 1 to
0 as an angle changes from 0 to 90 degrees or from 90 to 0 degrees. The right
triangle (with one 90 degree angles) helps us to define the sine and cosine.
Sine is the side (Y) opposite an acute angle (A) in a right triangle divided by
the diagonal or hypotenuse (r): sin A=Y/r. The cosine is the side (X)
adjacent, or next to, an acute angle, divided by the hypotenuse: cos A=X/r.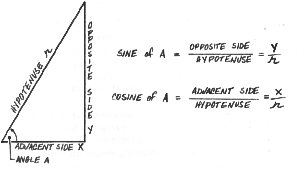
The famous Pythagorean theorem holds that the square of the length of the hypotenuse of a right triangle equals the sum of the squares of the lengths of the two other sides (r2** = X2** + Y2**, where 2** is square). Suppose we give r the value of 1. Remember that 1 x 1 equals 1. Of course r2** is still 1. Notice that with X2** at its maximum value of 1, Y2** is equal to 0.
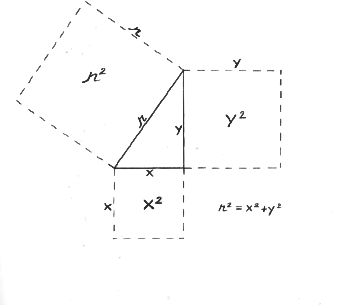
Thus when the cosine is at a maximum, the sine is 0, and vice versa. Sine and cosine, therefore, are opposites. If one is odd, the other is even.
Now imagine that we place our right triangle into a circle, putting angle A at
dead center and side X right on the equator. Next imagine that we rotate r
around the center of the circle and make a new triangle at various steps.
Since r is the radius of the circle, and therefore will not vary, any right
triangle we draw between the radius and the equator will have an hypotenuse
equal to 1, the same value we assigned it before. Of course angle A will
change, as will sides X and Y. Now the same angle A can appear in each
quadrant of our circle. If angle A does, the result is two result is two
non-zero values for both sine and cosine in a 360-degree cycle, which would
create ambiguity for us. But watch this cute little trick to avoid the
ambiguity.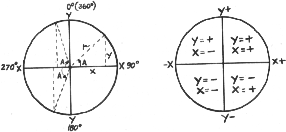
We can let all values of Y above the equator be positive; below the
equator, lets let them be negative. We can do the comparable thing with X,
except that we'll use the vertical meridian instead of the equator; then values
of X on the right side of our circle will be positive and those on the left
will be negative.
If we plot a graph of sine or cosine values for angle A versus degrees on the
circle, we get a wave. The cosine wave starts out at +1 at 0o
(360o), drops to 0 at 90o, plunges down to -1
at 180o and returns to +1 at 360o, the end of the cycle.
Meanwhile, the sine wave starts at 0, swells to +1 at 90o, drops
back to 0 at 180o, bottoms to -1 at 270o and returns to a
value of 0 at the completion of the 360-degree cycle. We really don't need the
triangle anymore (so let's chuck it!): the circumference will suffice.
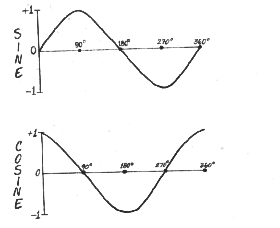Notice,
though, that the degree scale can get to be a real pain in the neck after a
single cycle. Roulette wheel, clock hands, meter dials, orbital planets,
components of higher frequency, and the like, rarely quit at a single cycle.
But there's a simple trick for shifting to a more useful scale. Remember the
formula for finding the circumference of a circle? Remember 2pi r? Recall
that pi is approximately 3.14, or 22/7. When we make r equal 1, the value for
the circumference is simply 2pi. This would convert the 90o mark to
1/2 pi, the 180o mark to 1pi (or just pi)...and so on. When we
reach the end of the cycle, we can keep going right on up the pi scale as long
as the baker has the dough, so to speak.
[8] But we end up with a complete
sine or cosine cycle at every 2pi.
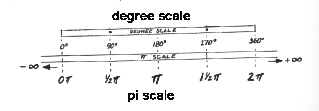
With regard to a single sine or cosine wave on the pi scale, what is amplitude? Recall that we said it was maximum displacement from the horizontal plane. Obviously, the amplitude of a sine or cosine wave turns out to be +1. But +1 doesn't tell us where amplitude occurs or even if we have a sine versus cosine wave--or any intermediate wave between a sine and a cosine wave. This is where phase comes in, remember. Phase tells where or when we can find amplitude, or any other point, relative to the reference; i. e., to zero.
Notice that our sine wave reaches +1 at 1/2pi, 2 1/2pi, 4 1/2pi... and so forth. We can actually define the sine wave's phase from this. What about the phase of a cosine wave? Quiz yourself, and I'll put the answer in a footnote.[9]
If someone says, "I have a wave of amplitude +1 with a phase spectrum of 1/2pi, 2 1/2pi, 4 1/2pi," we immediately know that the person is talking about a sine wave. In other words, our ideal system gives us very precise definitions of phase and amplitude. We can also see in the ideal how these two pieces of information, phase and amplitude, actually force us to make what Benjamin Peirce and his son Charles called necessary conclusions! Phase and amplitude spectra completely define our regular waves.
Now let me make a confession. I pulled a philosophical fast one here in order to give us a precise look at phase and amplitude. We know the phase and amplitude of a wave the moment we assert that it is a sine or a cosine wave. Technically, our definition is trivial. To say, "sine wave" is to know automatically where amplitudes occur on our pi scale. But let's invoke Fourier's theorem and apply it to our trivia. If a complicated wave is a series of sine and cosine waves, and those simple waves are their phase and amplitude spectra, then knowing the phase and amplitude spectra for a complicated wave means having a complete definition of it as well. Our trivial definition leads us to a simple explanation of how it is that phase and amplitude completely define even the most complicated waves in existence. It is not easy to explain the inclusiveness of phase and amplitude in the "real" world. But look at how simple the problem becomes in the ideal. First, phase and amplitude define sine and cosine waves. Second, sine and cosine waves define compound waves. It follows quite simply, if perhaps strangely, that phases and amplitudes define compound waves too. But there's a catch.
***
We can define the phase and amplitude of sine and cosine waves because we know where to place zero pi--0-- the origin or reference. We know this location because we put the 0 there ourselves. If we are ignorant of where to begin the pi scale, we don't know whether even a regular wave is a sine or a cosine wave, or something in between. An infinite number of points exist between any two loci on the circumference of a circle, and thus on the pi scale. The pure sine wave stakes out one limit, the cosine wave the other, while in between lie and infinite number of possible waves. Without knowing the origin of our wave, we are ignorant of its phase--infinitely ignorant!
Suppose though that instead of a single regular wave we have two waves that are
out of phase by a specific amount of pi? We still can't treat phase in
absolute terms. But when we have two waves, we can deal with their
phase difference--their relative phase value--just as we did in chapter
3 with the hands of the clock. And even though we may not be able to describe
them in absolute terms, we will not be vague in specifying any phase
differences in our system: our waves or cycles are out of phase by a definite
value of pi.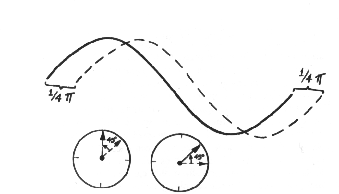 
If we transfer our waves onto the circle, we can visualize the
phase angle. In Fourier analysis, phase takes on the value of an angle.
What about relative phase in compound waves? Let's approach the problem by considering what happens when we merge simple waves to produce daughter waves. In effect, let's analyze the question of interference, but in the ideal. Consider what happens if we add together two regular waves, both in phase and both of the same amplitude. When and where the two waves rise together, they will push each other up proportionally. Likewise, when the waves move down together, they'll drive values further into the minus zone. If the amplitude is +1 in two colliding waves, the daughter wave will end up with an amplitude of +2, and its trough will bottom out at -2. Except for the increased amplitude, the daughter will look like its parents. This is an example of pure constructive interference; it occurs when the two parents have the same phase, or a relative phase difference of 0. The outcome here depends strictly on the two amplitudes, which, incidentally, do not have to be identical, as in the present example.
Next let's consider the consequences of adding two waves that are out of phase
by pi, 180 degrees, but have the same amplitude. They'll end up canceling each
other at every point, with the same net consequence as when we add +1 to -1.
The value of the daughter's amplitude will be 0.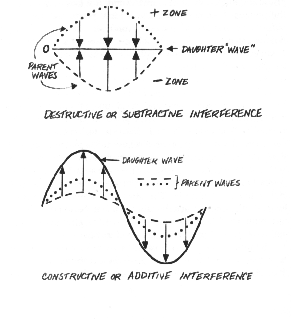 
In other words, the daughter
here won't really be a wave at all but the original horizontal plane. This is
an example of pure destructive interference, which occurs when the colliding
waves are of equal amplitude but opposite phase.
Now let's take the case of two waves that have equal amplitude but are out of phase by something less than pi; i.e., something less that 180 degrees. In some instances the point of collision will occur where sections of the two waves rise or fall together, thus constructively interfering with each other--like the interference that occurs when we add together numbers of the same sign. In other instances, the interference will be destructive, like adding + and - numbers. The shape of the resulting daughter becomes quite complicated, even though the two parents may have the same amplitude. Yet any specific shape will be uniquely tied to some specific relative phase value.
Now let's make the problem a little more complicated. Suppose we have two
regular ways, out of phase by less than pi; but this time imagine that they
have different amplitudes. The phase difference will determine where the
constructive and destructive interferences occur. Remember, though, that any
daughter resulting from the collision of two regular waves will have a unique
shape and size; and the resulting shape and size will be completely determined
by the phase and amplitude of the two parents. In addition, if we know the
phase and amplitude of just one parent, subtracting those values from the
daughter will tell us the phase and amplitude of the other parent.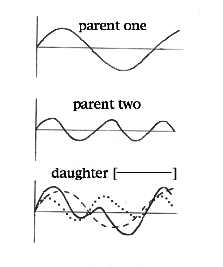
Suppose we coalesce three waves. The result may be quite complicated, but the basic story won't change: the new waves will be completely determined by the phase and amplitude of three, four, five, six or more interacting waves. Or the new compound wave will bear the phase and amplitude spectra that have determined completely by the interacting waves.
How does the last example differ from Fourier synthesis? For the most part, it doesn't. Fourier synthesis reverses the sequence of analysis.
The process is an abstract form of a sequence of interferences that produced the original compound wave. But the compound wave, no matter how complicated it is or how many components contributed to its form, is an algebraic sum of a series of phases and amplitudes.
***
A moment ago when we were talking about simple waves, I pointed out that we can figure out the values of an unknown parent wave if we know the phase and amplitude of the other parent and of the daughter. Why couldn't we do the same with an unknown compound wave? Why couldn't we, say, introduce a known simple wave, measure the phase and amplitude spectrum of the new compound wave, and then derive the unknown amplitudes and phases? It might take a long time, but we could do it, in theory. In fact, the holographer's reference wave is a kind of "known." The reference wave is a relative known in that its phase and amplitude spectra are identical to those of the object wave before the latter strikes the scene and acquires warps. The holographer's "known" results from coherency, from a well-defined phase relationship between the interfering waves. But the phase and amplitude spectra in the object wave upon reacting with those of the reference wave will completely determine the outcome of the interference. And the results of that interference, when transferred onto the hologram plate, create the hologram.
***
When dealing with waves, theoretical or physical, it is critically important to remember their continuous nature. True, the physicist tells us that light waves are quantized (come in whole units, not fractions thereof), that filaments emit and detectors absorb light as photons, as discrete particles. We can look upon the quantized transfer of lights as the emission or absorption of complete cycles of energy. But within the particle, the light wave itself is a continuum. And when we do something to a part of the continuum, we do it to all of it. If we increase the radius of a circle, the entire circle increases, if it remains a true circle. And we can see the change just as readily in a wavy plot. Also, the change would affect the outcome of the union of that cycle with another cycle. If we change, say, the Fourier coefficients on the second cosine wave in a series, we would potentially alter the profile of the compound wave. And the effect would be distributed throughout the compound wave. For, again, the components do not influence just one or two parts of the compound wave. They effect it everywhere.
The continuous nature of waves is the soberly scientific reason for the seemingly magical distributive property of Leith and Upatniek's diffuse hologram, wherein every point in the object wave front bore the warping effects of every point in the illuminated scene.
As I've mentioned numerous time, relative phase is the birthmark of all holograms and thus the central issue in hologramic theory of memory. Remember that phase makes a sine wave a sine wave and a cosine wave a cosine wave-- once there's any amplitude to work with. We can come to the very same conclusion for the compound wave: the amplitude spectrum will prescribe how much, but the phase spectrum will determine the distribution of that amplitude spectrum. Thus our profiles, yours and mine, are as recognizable on the surface of a dime as they would be on the face of Mount Rushmore. And your profile is uniquely yours, and mine, because of unique spectra of phase.
***
In this chapter, we have examined waves in the ideal. For only in the ideal can we free our reason from the bondage of experience. We are about to extend our thoughts into the hologram. Using reason, we will ease our minds into an abstract space where phase information lies encoded. This space is most often called Fourier transform space. The entry fee for crossing its boundaries is the Fourier transform (the equation I mentioned earlier in this chapter), the yield of Fourier analysis. We make the journey in the next chapter.
Internet contact:pietsch@indiana.edu