What is hologramic mind? What is the nature of the phase code? What is remembering? Recalling? Perceiving? Why does hologramic theory assert that physical parts of the brain, as such, do not constitute memory, per se? Why does hologramic theory make no fundamental distinction between learning and instinct? Why does hologramic theory predict the outcome of my experiments on salamanders? We have touched on these issues already, but only in an inferential, analogous and superficial way. Now we are on the brink of deriving the answers directly from hologramic theory itself. We will start by reasoning inductively from waves to the hologram and on to hologramic theory. Then, having done that, we will deduce the principles of hologramic mind.
***
The coordinate system we used in chapter 7 does exist on an ideal plane, true, but one we can easily superimpose on the surfaces we encounter in the realm of our experience. We can draw sine or cosine axes vertically on, say, the bedroom wall, or scribe a pi scale on a roll of toilet paper. If we equate sine values to something such as lumens of moonlight and place 29 1/2-day intervals between each 2pi on our horizontal axis, we can plot the phases of the moon. Alternatively, we could put stock-market quotations on the ordinate (sine or cosine axis) and years on the abscissa (our pi scale), and get rich or go broke applying Fourier analysis and synthesis to the cycles of finance. Ideal though they were, our theoretical waves existed in the space of our intuitive reality. I shall call this space "perceptual space" whether it's "real" or "ideal."
In the last chapter, I mentioned that in analyzing the compound wave (as a Fourier series of components regular waves, remember) the analyst calculates Fourier coefficients--the values required to make each component's frequency an integral part of a continuous, serial progression of frequencies. I also mentioned that the analyst uses coefficients to construct a graph, or write an equation. Recall that such an equation is known as a Fourier transform and that from Fourier transforms the analyst can calculate phase, amplitude and frequency spectra.
In everyday usage, "transform" is verb; it is sometimes a verb in mathematics, too. Usually, though, the mathematician employs "transform" as a noun, as the name for a figure or equation resulting from a transformation. Mathematical dictionaries define transformation as the passage from one figure or expression to another.[1] Although "transform" has specialized implications, its source, transformation, coincides with our general usage. In fact, a few mathematical transformations and their resulting transforms are part of our everyday experience. A good example is the Mercator projection of the earth, in which the apparent size of the United States, relative to Greenland, has mystified more than one school child and where Russia, split down the middle, ends up on opposite edges of the flat transform of the globe. We made use of transformation ourselves when we moved from circles to waves and back again. In executing a Fourier transformation, in creating the Fourier transform of components, the analyst shifts the values from perceptual space to an idealized domain known as Fourier transform space. In the old days (before computers did just about everything but wipe your nose) the analyst, more often than not, was seeking to simplify calculations. Operations that require calculus in perceptual space can be carried out by multiplication and division--simple arithmetic--in transform space. But many events that don't look wavy in perceptual space show their periodic characteristics when represented as Fourier transforms, and by their more abstract cousins, the Laplace transforms.
But my reason for introducing transform space has to do with the hologram. Transform space is where the hologramic message abides. The Fourier transform is a link to transform space.
We can't directly experience transform space. Is it a construct of pure reason? Alternatively, is it a "place" in the same sense as the glove compartment of a car? I really can't say, one way or the other. But although we cannot visualize transform space on the grand plain of human experience, we can still intuitively establish its existence. We can connect transform space to our awareness, and we can give it an identity among our thoughts.
Have you ever looked directly through the teeth of a comb? If possible, try it in soft candle light. Observe the halos, the diffraction of light at the slits. If you haven't done so, and you can't find a candle or a comb, try this instead. Hold the tips of your thumb and index finger up to your eye and bring them together until they nearly touch. You should be able to see the halos overlap and occlude the slit just a tiny bit before your finger and thumb actually touch. Those halos are physical analogs of Fourier and Laplace transforms. In principle, the edges of your fingers do to the light wave squeezing through the slit what the Fourier analyst does with numerical values: execute a transformation from perceptual to transform space. What is transformed? The answer: the image the light waves would have carried to your eyes if the halos hadn't mutually transformed each other.
If the transform exists, it can be shown the transform space containing it necessarily exists. I say this not to propound a principle but to give the reader an impressionistic awareness of transform space. We have to intuit the ideal domain much as we would surmise that a sea is deep because a gigantic whale suddenly burst upon its surface. At the same time, our own finger tips give us a sense of reality.
Now I will put forth a principle. Although we cannot literally visualize the interior of a transform space, we can grasp the logical interplay of transformed entities. And sometimes, with the correct choice of a specific transform space, we can greatly simplify the meaning of an otherwise arcane idea.
Let me demonstrate the latter point by introducing a process called convolution, whose ramifications and underlying theorem (convolution theorem) we will soon be calling upon.
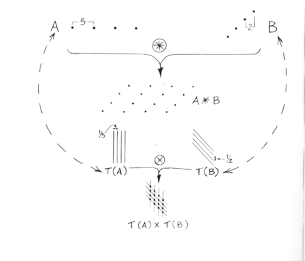
Convolution refers to the superimposition of independent sets, planes or magnitudes. Consider two initially separated set of dots, set A and set B, in perceptual space.[2] In the figure, A's dots line up on the horizontal axis at intervals of 5 units, say inches. Those of B are 2 inches apart and run obliquely up from left to right.
If we convolute A and B, we create a two-dimensional lattice. Using an asterisk to indicate the convolution operation, we can define the lattice as A*B, which we would read. "A convoluted on B." But what do we mean by convolute? And just how does convolution produce a lattice? The answer is rather complicated in perceptual space. But it's simple in a specific transform space, called reciprocal space (1/space).
We create 1/space from Fourier transforms. The Fourier transform of a line of dots is a grating; that is, a series of uniform lines. In 1/space the transform of A, let's call it T(A), is a grating made up of vertical lines whose spacings are the reciprocal of 5 inches--1/5 or 0.2 inches. The transform of B, T(B), is an array of oblique lines running downward from left to right, with 1/2 or 0.5 inch spacings (the reciprocal of 2 inches). We can superimpose the planes in T(A) and T(B). Because the transforms are lines, we can see directly that the superimposition of the two sets creates a grid, something we could not have envisaged with dots. The abstract operation corresponding to our superimposition is the same thing as uniting height and width to produce the area of a rectangle. This latter operation is multiplication. (A 2 inch vertical line and a 5 inch horizontal line produce a 2 by 5 rectangle.) And we can define the grid in transform space simply as T(A) x T(B).
Now let's take stock. First of all, perceptual and 1/space are reciprocal transformations of each other. Second, A and T(A) are transforms of each other, as are B and T(B). Therefore, the arcane and mysterious A*B--the lattice produced by convoluting A and B in perceptual space--is simply the reciprocal of T(A) x T(B). In other words, the asterisk in perceptual space is the equivalent of the multiplication sign in 1/space. We can't just up and call convolution multiplication. But we can see for ourselves that multiplication is the transform of convolution. Now multiplication is so much a part of our every day lives that we hardly think of it as an act of pure reason. But that's precisely what it is. And in opting for transform space, we made a small sacrifice in terms of intuition for a substantial gain in what we could avail to pure reason: simple arithmetic.
The convolution theorem, which we are about to employ, is the mathematical proof that indeed convolution is what we said it is--an arithmetic operation on transformation.[3] The critical lesson in our exercise is that while transform space is as remote as it ever was, it is far from incomprehensible. Fourier series have their corresponding Fourier transforms. And when attributes of waves do become incomprehensible in perceptual space, the appropriate transformation can put those attributes with the reach of reason.
***
When objects distort the phase and amplitude of light, the resulting warps add up not to an image of the object, but to the object's transform. The eye's optical system--cornea and lens--transform the transform into the object's image. The convolution theorem shows that the Fourier transform of the Fourier transform of an object yields the image. I'm truly sorry about the double talk. But the convolution theorem explains how the eye, a projector or a microscope can turn the wave's warps into an image: the objects transform the carrier waves, and the optical system of the eye transforms the transforms from transform to perceptual space. Now I must apologize for triple and quadruple talk. But think back a moment to the halos. They were transforms of transforms right at your very own finger tips. Because your eyes performed a third transformation, you saw the transforms instead of the edges of your fingers.
Just as the Mercator projection and the globe are different ways of representing the same thing, so Fourier transforms and Fourier series give us different perspectives on periodic phenomena. We can use what we learned in chapter 7 to understand the ideas we're formulating now. Think of the visible features of a face, a dewdrop or a stand of pines as a potential compound wave in three dimensions. The interaction between carrier waves and objects is comparable to Fourier analysis--to the dissection of the compound wave into a series of its components, except in transform space instead of perceptual space. In other words, the first transformation is much like producing a Fourier series. The second transformation--the one that occurs at the eye and shifts the components from transform to perceptual space--is comparable to Fourier synthesis, to synthesis of the series of components into a compound wave.
The hologram captures the transform of an object, not the object's image. The interference of object and reference waves shifts their components into transform space. To conceptualize the reaction, let's form our imagery around waves in perceptual space, but let's use reasoning alone for events that occur in transform space. Visualize the components of the compound object wave as being strung out in a row, as we might draw them on a piece of graph paper in perceptual space. Along come the reference wave and collide and interfere with each component. Each collision produces a daughter wave whose phase and amplitude are the algebraic sums of the phase and amplitude of the particular component plus those for the reference wave; or the reference wave and each components superimpose on each other. But the reactions take place in transform space, remember, and not in the perceptual space we use to assist our imagery. Therefore, we would observe not the image carried in the object wave, but an interference pattern, the transform--the hologram!
By imagining the components of a transform to be a Fourier series, we provide ourselves with something to "picture." This analogy could create the false impression that the object wave loses its continuity, that each component congeals into an isolated little unit in transform space. A continuum is a system in which the parts aren't separated, and the hologram is a continuum. We can appreciate its continuous nature by observing the diffuse-light hologram, any arbitrarily selected piece of which will reconstruct a whole image of the scene. Although the reference beam must act upon each of the object wave's components, as in our conceptualization, the interference pattern represents the whole.
Of course no interference patterns or holograms can develop unless the reference and object wave have a "well-define" phase relationship (coherency). Recall that the optical holographer, using Young's and Fresnel's old tricks, produces "well-defined" phase relationships by deriving object and reference waves from the same coherent source. What do we really mean, though, by "well-defined?" To say "coherency" or "in step" is merely to shift words around[4] without really answering the question. Instead, let me invoke a strange but powerful theorem of topology that will take us into the general meaning of "well-defined." The theorem is known as Brouwer's fixed-point theorem.
Fixed-point theorem is at the foundation of several mathematical ideas, and it is implicit in a great many more. The interested reader will enjoy Shinbrot's excellent article on the subject (see bibliography). Here, I will flat-footedly state the theorem without probing its simple but tricky proof[5].
Brouwer's theorem guarantees (no less) that in a continuous distortion of a system--as in stretching without tearing a rubber sheet, or stirring without splashing a bowl of clam chowder--at least one point must be in the same position at the end of the transformation as at the beginning. The point in question is the fixed point. Shinbrot describes how variants of the theorem have actually been used to predict contours of the ocean's floor from features on the water's surface. The absence of a fixed point is sufficient to deny a truly continuous relationship between two entities.
What is an object wave? In terms of frequency, it is the reference wave plus the changes imposed on it by the object. Before the object wave arrives at the scene, its frequency is identical to that of the reference wave. The object imposes a spectrum of new frequencies on the object wave., as we've in effect already said. But, invoking Brouwer's fixed-point theorem, we note that at least one point in the object wave comes out of the collision unchanged. In other words, the frequencies in the object wave will vary, but they'll vary relative to the invariant frequency at the fixed point. Because the reference and object waves once had identical frequencies, the fixed point in the object wave must have a counterpart in the reference wave. Through the fixed point, the frequency spectrum in the object waves varies--but relative to the frequency of the reference.
We must take note of an important difference between object and reference waves, namely the phase variation resulting from their different paths to the hologram plate. Let's call this phase variation D. D will vary for each object component vis-à-vis the reference. But because of the fixed point, one of those Ds will have the same value before and after the interference of reference and object waves; and all the other waves will vary relative to the invariant D. Variation relative to some invariant quantity is the general meaning of "well-defined," including "well-defined" phase relationships in interference phenomena. And a well-defined spectrum of Ds in transform space is the minimum condition of the hologram. The minimum requirement is a fixed-point relationship between object and reference waves. Minimally then, a specific hologram is a particular spectrum of well-defined Ds in transform space.
Reconstruction of the image from the hologram involves transforming the transform, synthesizing the original compound wave and transferring the visible features of the scene back to perceptual space. This statement is a veritable reiteration of how the object originally communicated its image. In theory, the hologram regenerates what the object generates. In order for a wave to serve reconstruction, it must interact with all the components and must satisfy the fixed-point requirement.
***
What is memory, then? If we transfer the principles we've developed to hologramic theory, we can define a specific memory as a particular spectrum of Ds in transform space. Again, what are Ds? They are phase differences --relative values, relationships between and among constituents of the storage medium--of the brain! Thus in hologramic theory, the brain stores mind not as cells, chemicals, electrical currents or any other entity of perceptual space, but as relationships at least as abstract as any information housed in the transform space of a physical hologram. The parts and mechanisms of the brain do count; but the Ds they establish in transform space are what make memory what it is. If we try to visualize stored mind by literal comparisons with experience, we surrender any chance of forming a valid concept of the hologramic mind, and quite possibly we yield all hope of ever establishing the existence of the noumenon where the human brain stores the human mind.
***
In hologramic theory, the utilization of a series of Ds during overt or covert behavior, in recall--or thoughts or feelings or whatever--is transforming the transform into perceptual space.
A percept, the dictionary tells us, is what we're aware of through our senses or by apprehension and understanding with the mind. In hologramic theory, a percept is a phase spectrum, a series of Ds in perceptual space. An active or conscious memory, a reminiscence, is a back-transformed series of Ds that have moved from transform to perceptual space. In terms of the phase code, then, perception and reminiscence involve the same basic information, the difference being the source of the Ds: the percept is analogous to image generation by an object, while the activated memory is analogous to the reconstruction from the hologram. Both synthesize the message in the same theoretical way. As Karl Pribram asserted in a lecture some years ago, memory regenerates what perception generates.
The specific character of the activated memory depends on the particular readout. A useful analogy here would be to the holographer's use of light instead of sound to decode an acoustical hologram, except that the nervous system has many more options than the engineer. The activating signal would determine the special features of the transformed transform, but the phase spectrum--the basic series of Ds--would be the same whether imagination or the fist punched somebody in the nose. In other words, through the code in transform space, behavior is the transduced version of perception. I'll expand on this idea more fully in a later chapter, after we've extended hologramic theory beyond where we are now. But we've already come far enough for me to say that hologramic theory provides a unified view of the subjective cosmos. There's not a box over here marked "perception" and one over there labeled "behavior" with fundamentally different laws of Nature governing each. Just as one gravity affects all bodies falling to earth, feathers or bowling balls, so one system of abstract rules works ubiquitously when it comes to facets of the mind.
***
Frequency of a traveling wave in perceptual space depends on time. Thus the Hz (herz) value specifies cycles per second. In an interference pattern, however, frequency refers to how many stripes or beats occur in a given area. And whereas frequency assumes a temporal character in perceptual space, it can take on spatial meaning in transform space.
We can draw an insightful corollary from the preceding paragraph. The phase difference between two interfering sets of waves determines the frequency of beats or stripes within the interference pattern. An intimate relationship exists, then, between phase and frequency. In FM (frequency modulated) radio, a specific message is a particular spectrum of phase variations. In waves with frequency independent of amplitude, as in the nervous system, the phase-difference spectrum in transform space is the stored memory. Earlier we used Metherell's phase-only acoustical holograms to postulate phase codes as the character of hologramic mind. Here, however, we have just deduced this conclusion directly from the theory itself.
Karl Pribram suggested in the 1960s that visual perception is analogous to Fourier transforms. He had in mind the hologram. More recently, a couple named De Valois and their collaborators developed a computerized system for calculating Fourier transforms of checkerboards and plaid patterns. They used their system to analyze neurons of the visual cortexes of monkeys and cats. Are the cells encoded to perceive structural elements of the patterns? No! The neurons of the visual cortex respond to Fourier transforms of the patterns, rather than to the patterns' structural elements. The DeValois results "were not just approximately correct but were exact" within the precision of their system.[6] As Pribram had previously predicted, the retina sends the brain not a literal rendition of the image, but a transform of the image. To phrase this observation in the language of hologramic theory, the phase codes stored in cells of the visual cortex transform the transform into images in the perceptual space of the conscious mind.
***
Mathematicians often discover the properties of their theorems when they manipulate equations or bring different terms together in novel ways. We are about to do analogous things with phase codes. Instead of equations, though, we will do our "calculations" in the "real" world, with pictures.
Consider these two identical sets of rings (Fresnel rings, they're called).
.......
If we superimpose them out of phase, they produce moiré patterns
--interference fringes or beats:
Just how many beats there are per unit--frequency--depends precisely on how far out of phase the two. In the moiré patterns out of phase depends on how far apart the centers of the central ring lie. The stripes (whose thickness is inversely proportional to the phase difference) represent the phase code in transform space
Are the stripes memories of the phase spectrum in the rings? The answer is yes, when the stripes reach a high frequency. But let's not take my word for it. Let's turn the statement into an hypothesis and test it. If stripes encode for rings, we should be able to back-transform rings using stripes alone. We ought to be able to superimpose stripes on a set of rings and make new rings in perceptual space. Here's what happens if we take a set of fine (high frequency) stripes and lay them on our rings
.......
New rings indeed back-transform into perceptual space when we superimpose only stripes on our rings.
What do we really mean by our stripes? They are beats, yes. But stripes are periodic patterns of light and dark, a harmonic array of alternating densities. Given this, the memory of rings shouldn't literally be confined to stripes as such. The memory is a periodicity, a wavy logic. We should be able to back-transform rings with, say, dots. Here's what we get when we carry out the experiments:
For an enlargement see footnote [8]
***
I've presented the dot experiment for an additional reason. Maybe I was just lucky with the rings? Perhaps the various dots are fortuitously spaced so as to interact with the correct arcs on the rings. If you look carefully at the back-transformed rings, you'll see that they're not all identical. In fact, those on opposite sides of either the vertical or horizontal axes, and thus on perspective arcs of the same circles, are mirror images of each other: where one ring has a dark center, the corresponding ring is light. If the "maybes" in the above speculations were correct, these rings would have been identical, which they plainly are not.
And the dots show us something I hadn't foreseen at all, but can't resist
pointing out here. Let me show you a blown up set of dots at the edge where
there aren't any rings. 
I mentioned in
chapter 4 that we humans often have a hard time remembering something exactly
as we originally experienced it. Have you ever fumbled around with several
vivid recollections that are similar but not identical and couldn't decide on
the exact one, e.g. the first name of a bygone author, actor, sweetheart?
Even our simple optical patterns seem to have this difficulty. A quick peek at
the notes or a fresh percept for comparison can solve the problem much more
reliably than memory alone. Likewise, with our dot system we merely have to
compare the various readouts with the center ring to ascertain which
recollection precisely corresponds to the original scene.
In hologramic theory, reasoning, thinking, associating or any equivalent of correlating the ring is matching the newly transformed transform with the back-transform. (The technical term for such matching is autocorrelation.)
***
Let's shift our focus back to the nature of the phase code, which in our ring system is the preservation of ring information by periodic patterns. The ring memory is not limited to dots and stripes. When we react rings with too great a distance between their centers (if their center rings do not overlap), we do not produce stripes. Instead, something interesting happens. Notice that if we get the centers far enough apart, rings form in the readout:
;
Built into the higher frequency rings is a memory of rings closer to the center. Let me explain this.
First of all, as I've pointed out, the phase code isn't literally dots or stripes or dots[7] but a certain periodicity; i. e., a logic! Our rings are much like ripples on a pond; they expand from the central ring just as any wave front advances from the origin. Recall from Huygen's principle that each point in a wave contributes to the advancing front. The waves at the periphery contain a memory of their entire ancestry. When we superimpose sets of rings in the manner of the last figure, we back-transform those hidden, unsuspected "ancestral " memories from transform to perceptual space. The last picture demonstrates that no necessary relationship exists between the nature of a phase code and precisely how that phase code came into being. The "calculation" represented by the picture shows why hologramic theory fits the prescriptions of neither empirical nor rational schools of thought. In the experiments where we superimposed rings on rings the system had to "learn" the code; the two sets of rings had to "experience" each other within a certain boundary in order to transfer their phase variation into transform space. But the very same code also grew spontaneously out of the "innate" advance of the wave front. These, reader, are the reasons why I would not define memory on the basis of either learning or instinct. As trees are irreducibly wood, memory is phase codes: whether the code is "learned" or "instinctive" has no existential bearing on its mathematical--and therefore--necessary features.
***
Consider something else our stripes, dots and rings reveal about the phase code. We can't assign memory to a specific structural attribute of the system. In hologramic theory, memory is without fixed size, absolute proportions or particular architecture. Memory is stored as abstract periodicity in transform space. This abstract property is the theoretical basis for the predictions my shufflebrain experiments vindicated, and for why shuffling a salamander's brain doesn't scramble its stored mind. My instruments cannot reach into the ideal transform space where mind is stored. For hologramic mind will not reduce directly to the constituents of the brain.
Internet contact:pietsch@indiana.edu