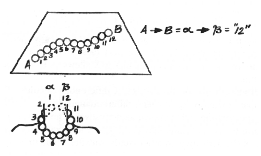
 Suppose the distance from A to B is 12 pearls.
Suppose the distance from A to B is 12 pearls. NORBERT WIENER, the mathematician who founded cybernetics just after World War II, once observed about computers, "the energy spent per individual operation is almost vanishingly small," and he went on to warn contemporary science that "Information is information, not matter or energy. No materialism which does not admit this can survive at the present day."[1] Reduction of the message to the medium, he realized, would eventually force scientists to do something they wouldn't (and don't) want to do: repeal the powerful and indispensable laws of thermodynamics. Wiener of course knew that information can't exist on nothing. But to stamp your foot and insist that information and mass-energy are one in the very same thing would quickly put the natural sciences in an untenable philosophical position. Wiener knew in his bones that abstract relationships--ratios-- within mass-energy are what create, encode and store information, not matter or energy as measured by the pound or erg.
With respect to the hologram, we have already arrived at Wiener's conclusion ourselves: functional relationships within the media encode phase information. Thus quite different physical entities, widely varying absolute energies or basically dissimilar chemical reactions can construct, store and decode the same hologram--as information! Initially, and by force of implication, we extended this principle of information to hologramic mind. But at the end of the last chapter, we came to this same conclusion directly, from hologramic theory, itself. A mind, the theory asserts, is not specific molecules, particular cells, certain physiological mechanisms or whatever may serve as the mind's media. Mind is phase information--relationships displayed in time and in perceptual space but stored as a function of time and a function of perceptual space in transform space. We have a subtle but pivotal distinction to make, then: molecules, cells, mechanisms, and the like are necessary to create, maintain or display those phase relationships. But the relationships are not reducible to a molecule, cell or mechanism any more than the message on a printed page is reducible to ink and paper. And when we investigate mind in molecules, on cells or via mechanisms, we have to be very careful about the words we chose to describe our results. Conjugates and equivalents of the verb "to do" are what we want when we employ test tubes, microscopes or electrodes. But when we ask the mind is, then we must turn to theory.
Does hologramic theory demand that different constituents and mechanisms of brain house memory? As Bertrand Russell maintained, theory is general. The moment we begin to talk about specific parts, we shift to the particular, to issues the experimentalist (e. g., the brain shuffler) must pursue. What hologramic theory does, though, is account for,say, how more than one class of things or events can serve as a medium for the very same memory. If a protein encodes the same spectrum of phase variations as occur in, for instance, a feedback loop around the hippocampus, then the same memory exists in or on both the protein and the feedback loop.
Again: the test tube, the microscope and the electrode work only in perceptual space. Of course, this restriction doesn't minimize their value, nor does it undermine the importance of experience. But to get inside the hologramic mind, to unravel its logic, to discover its plan, to figure out how the mind actually works, we must use abstract tools. Only with reason, with an assist from imagination, can we cross the boundary between the real and the ideal.
Yet we can use our imaginations to resynthesize in our own reality the relationships our reason uncovers in realms beyond. We were doing this with transforms, convolution theorem and Fourier series. The holographic engineer also does it with reconstruction beams. Pribram did it in the living, remembering brains of monkeys. I did it with shufflebrain, albeit unwittingly at first. If we use the theory with art as well as science, and exercise a little humility en passant, not only can we extend our comprehension beyond experience, but we can avoid imprisonment within the ideal and exile from our own reality. Hologramic theory does not dispense with the brain. Activated, mind perceives, thinks and drives behavior in perceptual space.
In its present form, though, hologramic theory will not serve our needs. Fourier transform space is too cramped for us to appreciate, for instance, the similarities and differences between our own mental cosmos and the minds of other creatures. Fourier transform space is too linear to explain the nonlinear relationship between the time we measure by the clock and the intervals that elapse in dreams, for example. Nor in Fourier and kindred transform spaces can we readily envisage the smooth, continuous movement of information from sensations to perceptions to memories to behavior to whatever. How can the information be the same while the events retain their obvious differences? Described only in the language of Fourier theorem, mind seems more like the inner workings of a compact disc player than the subjective universe of a living organism. If the reader has already felt that something must be wrong with our picture, it's because he or she knows very well that we mortals aren't squared-off, smoothed-down, case-hardened, linearly perfected gadgets.
***
Thus far, the constraints on our understanding have two main causes. First, our theory is now anchored to the axioms and postulates of Euclid's geometry. Second, we haven't yet given sufficient theoretical identity to the particular, having been too preoccupied with escaping from the particular to give the attention it really deserves. In this chapter, I will first reassemble hologramic theory free of assumptions in previous chapters. Towards the end, I will draw the realm of the particular into our discussion. Ready? Take a deep breath!
***
June 10, 1854 is an noteworthy date in the history of thought. It was also a momentous day in the brief life of mathematician Georg Friedrich Bernhard Riemann whose discoveries were crucial to Albert Einstein.[2] It was when Riemann stood before the distinguished professors of Göttingen's celebrated university to deliver his formal trial lecture as a probationary member of the faculty. Entitled, "On the Hypotheses Which Lie at the Foundations of Geometry," the lecture attacked a dogma that had ruled rational belief, "From Euclid to Legrendre," asserted the twenty-eight year old Privat-dozent. [3]
"It is well known," he continued, "that geometry presupposes not only the concept of space but also the first fundamental notions for constructions in space as given in advance. It gives only nominal definitions for them, while the essential means of determining them appear in the form of axioms. The relation [logic] of these presuppositions [the postulates of geometry] is left in the dark; one sees neither whether and in how far their connection [cause-effect] is necessary, nor a priori whether it is possible."
In the detached bon ton of scholars then and now, Riemann in effect was telling his august audience (including no less that his mentor, Karl Friedrich Gauss) that mathematicians and philosophers had flat-footedly assumed that space is just there. Like the gods in The Iliad who had an external view of the mortal realm, mathematicians and philosophers had inspected space in toto, had immediately brought rectilinear order to the nullity, with the flat planes of length, width and height, and thereby had known at a glance how every journey on a line, across a surface or into a volume must start, progress and stop. Geometric magnitudes--distance, area, volume--plopped inexorably out like an egg from laying hen's cloaca.
Ever since Newton and Leibnitz had invented calculus, infinitely small regions of curves had been open to mathematical exploration; but points on a straight line had eluded mathematician and philosopher, alike. Riemann doubted that the same fundamental elements of geometry--points--could obey fundamentally different mathematical laws in curves versus lines. He believed that the point in flat figures had become an enigma because geometry had been constructed from the top down, instead of from the bottom up: "Accordingly, I have proposed to myself at first the problem of constructing a multiply extended [many dimensional] magnitude [space] out of the general notions of quantity." He would begin with infinitely small relationships and then reason out the primitive, elemental rules attending them, instead of assuming those rules in advance. Then, not taking for granted that he knew the course before his journey into the unknown had begun, he would, by parts, follow the trail he had picked up, and he'd let the facts dictate the way.
To the best of my knowledge, the first formal principle of quantity remains to be found, if one really exists at all. Even Riemann's genius had to be ignited by intuition. Intuitively speaking, the basic notions of quantity imply measuring something with something else. As in our optical transform experiments in the last chapter, measuring to Riemann, "consists in superposition of the magnitudes to be compared." As in the case with the reference and object waves in the hologram, superposition of the two magnitudes or quantities occurs "only when the one is part of the other."[4] Riemann was speaking about continuity in the most exactingly analytic sense of the word.
Where can we find continuity? More important, how can we guarantee its existence in the relationship of, say, X and Y? To satisfy Riemann's requirements, we would have to show that at least one of the elements involved necessarily affects the other. Thus a frog on a lily pad won't do, especially if the animal is just sitting there enjoying the morning sunshine. We would have to find out if any change in either the animal or the plant forces a concomitant variation in the other. Thus the first requirement for establishing continuity is to get away from static situations and focus on dynamic--variable--relationships. Do they change together?
Suppose, though, that one unit of change in X procures a one-unit change in Y; that Y=X. If we graph the latter, the plot will look like a straight line. In a linear relationship, the ratio of Y to X, of course, remains constant no matter how large or small the values become. This constancy made mathematicians before Riemann shy away from points on the straight line. For an infinite number of points exist between any two points on a line; even as the values of X and Y approach zero we never close the infinite interval between two points on a straight line.
The curve is quite another story. What is a curve? My handworn 1964 edition of Encyclopedia Britannica characterizes it as "the envelop of its tangents." Remember that on a circle, the very embodiment of curvature, we can draw a tangent to a single point on the circumference. The same thing holds for tangents to a curve; and we do not draw a tangent to a straight line. Like the sine or cosine, the tangent is a function of an angle.[5] We might think of a tangent as a functional indicator of a specific direction. The points on a straight line all have the same direction; therefore, a tangent to a straight line would yield no information about changes in direction (because the directions are all the same). Neighboring points on a curve, by contrast, have different relative directions. Each point on a curve takes its own specific tangent. And the tangent to the curve will tell us something about how the directions of one point vary relative to neighboring points.[6]
Imagine that we draw a tangent to a point on the X-Y curve. The bend in the curve at that point will determine the slope of the tangent. If we could actually get down and take a look at our X-Y point, we'd find that its direction coincides with our tangent's slope. Of course, we can't reach the point. But we can continuously shrink X and Y closer and closer to our point. As we get nearer and nearer to the point, the discrepancy between the curve and the slope of the tangent becomes smaller and smaller. Eventually, we arrive at a vanishingly tiny difference between curve and tangent. We approach what Isaac Newton called--and mathematicians still call--a "limit" in the change of Y relative to X. The limit--the point-sized tangent--is much like what we obtain when we convert the value of pi from 22/7 to 3.14159...and on and on in decimal places until we have an insignificant but always persisting amount left over. The limit is very close to our point. The continuous nature of the change in Y to X permits us to approach the limit.
Finding limits is the subject of differential calculus. The principal operation, aptly called differentiation, is a search for limit-approaching ratios known as derivatives. The derivative is a guarantee of continuity between Y and X at a point. The existence of the derivative, in other words, satisfies Riemann's criterion of continuity: Y is part of X. The derivative is strictly a property of curves. For the derivative is a manifestation of changing change in the relationship of a point to its immediate neighbors. Derivatives, minuscule but measurable ratios around points, were the basis from which Riemann developed the fundamental rules of his new geometry.
Derivatives are abstractions. And, with one valuable exception, we can gain no impression of their character by representing them in perceptual space. The exception, though, will permit us to "picture" how Riemann discovered measurable relationships among points.
The exceptional derivative signals itself in mathematical discourse by an italicized lower case e. [7] The numerical value of e is 2.718218...(to infinity). It goes on and on forever, like pi. The curve made up of e is smooth in contour and sigmoid (S) in shape, and it relates Y to X, as follows: Y = eX. That is, Y equals 2.718218....if X is 1; the square of e if X is 2; the cube of e if X is 3....and so forth to infinity. In the latter expressions, e to some power of X is a function of X, meaning that e has a variational relationship to Y. But what makes e so very special to us is that its derivative equals the function. In other words, when we look at a sigmoid curve, we see what we would see if we could actually plot Y = eX at a single point. Thus what we represent in perceptual space as a S-curve has validity for what we can't actually see at the point. [7a]
Imagine now that we have undertaken the task of exploring geometric figures. Assume that, like Riemann, we don't know the rules in advance and that our only metering device is e. To assist our imagery, envisage e 's as a string of pearls. Assume that we can bend and flex the string, increase or decrease the number of our e 's but can neither break nor stretch the string.
Okay, now suppose we come upon a flat surface and find two points, A and B. What would be the shortest distance between them? Remember, we must base our answers only on what we can measure. Gauged by our string of pearly e 's, the shortest path is the least number of e 's between A and B.
 Suppose the distance from A to B is 12 pearls.
Suppose the distance from A to B is 12 pearls.
Now imagine that we put our string of pearls around some body's neck. Clearly, a path of 12 pearls remains a path of 12 pearls even though the new surface (neck) has a different shape from the first. Or with e 's as a gauge, we can relate a flat surface to a curved surface merely by finding their equivalents--the number of e 's. In our imaginary universe, round and square thus become variants of a common theme.
Let's return to the flat surface. This time, imagine that we run the hypotenuse of a large right triangle from A to B. When we lay the pearls between A and B, we find that the string fits very loosely on the hypotenuse. Even though we can always count pearls, we cannot gauge the hypotenuse very accurately because of the poor fit.
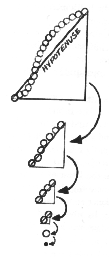
Suppose though that we reduce the number of e 's in our string and proportionally shrink the triangle; we continue to make the string and the triangle smaller and smaller but always remembering to take measurements by counting e 's. As we proceed, the slack between the string and the hypotenuse becomes smaller and smaller and eventually becomes so small as to be insignificant. Despite all the proscriptions of tradition, the hypotenuse--which looks like a straight line--has begun to approach a limit, relative to our pearls. We don't want to assert that the hypotenuse and our pearly e 's are "the same thing." If we do, we create the intolerable contradiction that the hypotenuse and the S-curve look alike, which we can see is false. But at infinity, the one is part of the other. The measurable part in question is little old e. Thus points in the hypotenuse have a measurable feature in common with points in our string of e 's. And that measurable feature is curvature.
Riemann also arrived at such an inference, although in a much more general, inclusive and rigorous way. "About any point," he discovered, "the metric [measurable] relationships are exactly the same as about any other point." A straight line, a flat surface or a rectilinear space consists of the same fundamental elements as a curve, circle or sphere; and magnitudes--round or square (pie or cornbread)--"are completely determined by measurements of curvature." Riemann showed that "flatness in smallest parts" represents "a particular case of those [geometric figures] whose curvature is everywhere constant." Flatness turned out to be zero curvature. In other words, a geometric universe constructed from elementary measurable relationships among points becomes an infinite continuum of curvatures, positive and negative, as well as zero.
Riemann demonstrated that "the propositions of geometry are not derivable from general concepts of quantity, but...only from experience." Out the window went the absolute prohibition against dealing with infinitely small regions of straight lines.[8] Out went the notion that parallel lines never! never! cross. Out went the universal dogma of even our own day that the shortest distance between two points is absolutely always the straight line.
The prohibition against points on lines was an artifact of trying to approach points from a flattened-down, squared-off, cut-straight universe; and the same had been true about parallel lines. And where did we ever come up with the idea that the shortest distance has to be the straight path? The argument in favor of straight lines has had its epistemological justification in the peroration of my little sister's ontology: "Because the teacher said!"
But how can all this Riemann stuff really be? Why don't our bridges all fall down?
The irony is that Riemann's system is not anti-Euclidean. As I pointed out earlier, Euclid's geometry belongs to the realm of experience. It is the geometry we invent and use for distances neither very great nor very small; for uncomplicated planes; for simple spaces; for universes of non-complex dimensions; for standard forms of logic (like Aristotle's). With Riemann's system as a guide, Euclid's propositions even acquire a valid a priori foundation. [9] Their limitations no longer dangerously hidden from us, Euclid's rules can serve our needs without tripping us up. Infinitesimal regions on a straight line are beyond the Euclidean approach, and thus we must use a different method for handling them; parallel lines don't intersect on a Euclidean plane; we can safely lay railroad track in the conventional manner. As far as the shortest distances thing is concerned, we may keep the protractor, the ruler and the T-square for geometric operations within the ken of experience. For in a Riemannian universe, the shortest distances between points is the path of least curvature. In the Euclidean realm of experience, that least curvature approaches zero curvature, and it coincides with what looks like a straight line.
I once worked on a crew with a graduate student in philosophy we all called Al-the-Carpenter. (His thesis was "God is Love.") Older and wiser and more generous than the rest of us, Al let scarcely a day pass without an enlightening observation or an unforgettable anecdote. "I met a little boy this morning," he once told us as we gathered around the time clock, "while I was making picnic tables outside the recreation hall. 'Is the world really round?' the little boy asked me. 'To the best of my knowledge,' I answered. 'Then tell me why you cut all the legs the same length. Won't your tables wobble?'"
"Yes," his tables would wobble, Al had replied. But the wobble would be infinitesimally tiny. The smile he usually wore broadened as he lectured like a latter-day Aristotle. "If you want to hear philosophical questions, pay attention to the children."
***
A theory constructed to fit the planes of experience will show its wobble when we invoke it on a very large, exceedingly small or extremely complex body of information.
Until now, we have viewed hologramic mind along Euclidean axes. But an understanding of hologramic mind requires the freedom only Riemann's simple but powerful ideas can give it.
***
Riemann's name and influence pervade mathematics (e.g., Riemann surfaces, Riemann manifolds, Riemann integrals, Riemannian geomery) for reasons that are evident in his qualifying lecture. The seeds of his subsequent work are present there. The elementary relationships at points later became the means by which scientists learned to conceptualize invariance. Toward the completion of the lecture, Riemann even anticipated general relativity. (Einstein's 4-dimensional space-time continuum is Riemannian.) Where did Riemann's insight come from? What intuitive spark caused his genius to push against the outermost fringes of human intellectual capability? I'm not sure I have the answer and only raise the question because I think my personal suppositions (i.e., hunch) will help us in our quest of hologramic mind.
***
Riemann, I believe, had a vivid concept of what I'll call "active" zero, the 0 between +1 and -1: the set we cross when we overdraw from the checking account--not the zero an erudite philosophy professor of mine, T. V. Smith used to call "what ain't." Judging from his own writings, Riemann seemed to have a crystal-clear intuitive idea of zero space--and even negative space![10] Let's try to develop a similar concept, ourselves. But so that what we say will have theoretical validity, let me make a few preliminary remarks.
There's a principle in logic known as Gödel's incompleteness theorem. The latter theorem tells us that we cannot prove every last proposition in a formal system. It's a sort of uncertainty principle of the abstract. We'll obey this tricky-- but powerful-- principle by always leaving at least one entire dimensional set beyond our reach. In fact, let's throw in two uncountable dimensions: negative and positive infinity which, by definition, are sets beyond our reach whether we admit our limitations or not. (Plus and minus infinity are by no means new ideas, incidentally.)
Consider a pretzel and a doughnut (or a bagel, if you're avoiding sweets). To keep the discussion simple,
imagine them on a plane. Our doughnut has two apparent surfaces, the outside
and the lining of the hole (Riemann called it a doubly connected surface). Our pretzel has four surfaces ("quadruply" connected) : one for each of the
three holes, plus the exterior. Let's assume (with Riemann) that all things with the same
number of surfaces belong to the same topological species, and let's not fret about whether
the doughnut is round, oval or mashed down on one side. 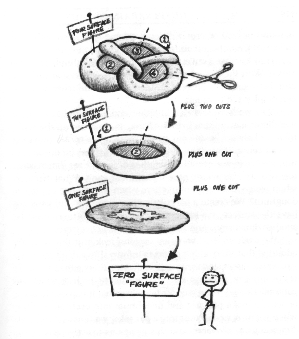 Also, let's consider
surface to be a manifestation of dimension.
Also, let's consider
surface to be a manifestation of dimension.
How can we convert a pretzel to a doughnut and vice versa? With the pretzel we could make the conversion with two cuts between two apparent surfaces. To go the other way, we (or the baker) can employ the term join.--two joins to regenerate a pretzel from a doughnut.
We've said that at either end of our universe there's a dimension (surface) we can't reach, positive and negative infinity. Thus, as we move up the scale (by joining), there's always one dimension more in the continuum than we can count. If we actually observe two surfaces on the doughnut, we know our overall system (or ideal universe) has at the very minimum three positive dimensions: the two we can count and the one we can't.[10a] What happens when we move in the other direction--when we apply (or add) one cut to our doughnut? We create a pancake with a single (singly connected) surface. But since we have the one countable surface, we know that still another surface must exist in the negative direction. And in the latter dimension is active zero.
Wait! We can't do that! you may insist. But look at it like this. We admitted that we can't count to infinity, right? If we don't put those uncountable dimensions on either end of our universe, then we end up in a genuine bind: either we can't count at all or we can reach unreachability. We can see for ourselves that we can cut or join--add and subtract (count)--to make pretzels and doughnuts out of each other. But to assert that we can reach unreachability may be okay for a preacher, but it's preposterous for a scientist.
Suppose we add a cut to a pancake--eat it up, for instance. Where are we? We now have another goofy choice: between active zero (zero surface) and "what ain't." We can't define "what ain't"; or, if we do define "what ain't" by definition, it won't be "what ain't" anymore. If we don't define it, it disappears from the argument, leaving us with good grammar and the zero-surfaced figure. And we can define the zero-surfaced dimension from our counting system: the dimension sandwiched between the one-surfaced pancake and the minus-one dimension.[11]
If we can conceive of a zero-dimensional surface, we can certainly appreciate a zero-curvature without making it "what ain't." And the zero-curvature, as part of the continuum of curvatures, is the curvature of the Euclidean world of experience.
***
Before we put hologramic mind into a Riemannian context, I would like to emphasize three important principles.
Now let's make a preliminary first fitting of hologram mind to the world of Riemann.
***
In terms of our search, a periodic event in perceptual space is a transformation, as a least curvature, to any other coordinates within the mental continuum. The same thing would be true of a series of periodic events. Since phase variation must be part of those events, memory (phase codes) becomes transformable to any coordinates in the mental continuum. A specific phase spectrum--a particular memory--becomes a definite path of least curvature in transformations from sensations to perceptions to stored memories to covert or overt behaviors, thoughts, feelings or whatever else exists in the mental continuum. If we call on our e 's for imagery, the least pearly path will not change merely because the coordinates change. Behavior, then, is an informational transform of, for instance, perception.
Transformation within the Riemann-style mental continuum is the means by which hologramic mind stores itself and manifests its existence in different ways. But we need some device for carrying out the transformation in question. For the latter purpose, I must introduce the reader to other abstract entities, quite implicit in Riemann's work but not explicitly worked out until some time after his death. These entities are known as tensors.
***
The mathematician Leon Brillouin credits the crystal physicist W. Voigt with the discovery of tensors in the world of mass-energy.[12] It's no news that a crystal's anatomy will deform in response to stress or strain. But what stunned Voigt was that certain relative values within the distorted crystal remained invariant before and after the deformation. Tensors represent those invariant relative values. Like Riemann's invariant curvature relationships, tensors survive transformation anywhere, any place, any time. Just in time for Einstein, mathematicians worked out and proved the theorems for tensors. In the process they found tensors to be the most splendid abstract entities yet discovered for investigating ideal as well as physical changes. Tensors provided mathematicians with a whole new concept of the coordinate. And tensors furnished Einstein with a language in which to phrase relativity, as well as the means to deal with invariance in an ever-varying universe. As to their power and generality, Brillouin tells us: "An equation can have meaning only if the two members [the terms on either side of the equals sign] are of the same tensor character."[13] Alleged equations without tensor characteristics turn out to be empirical formulas and lack the necessity Benjamin Peirce talked about.
Tensors depict change, changing changes, changes in changing changes and even variations of higher orders. Conceptually, tensor resemble relative phase. Tensors relationships transform in the same way that relative phase does. This transformational feature affords us an impressionistic look at their meaning.
Do you recall the dot transform experiments from the last chapter:

 Notice the diagonal arrangement of both the dots and the rings. If we rotate
the rings so as to bring them into a horizontal orientation (tilt your head), the dots also take on a
horizontal arrangement.
Notice the diagonal arrangement of both the dots and the rings. If we rotate
the rings so as to bring them into a horizontal orientation (tilt your head), the dots also take on a
horizontal arrangement.
The rings and dots are transforms of each other. The fundamental direction of change remains constant in the transform as well as its back-transform. And during rotation, the basic orientation of the rings and dots--relative to each other--remains invariant. Absolute values differ enormously. But as we can see for ourselves, the relative values transform in the same way. This is the cardinal characteristic of the tensor: it preserves an abstract ratio independent of the coordinate system. If we stop to think about it, we realize that if tensors carry their own meaning wherever they go, they should be able to define the coordinate itself. And so they do.
Ordinary mathematical operations begin with a definition of the coordinate system. Let's ask, as Riemann did, what's the basis for such definitions? With what omniscience do we survey the totality of the real and ideal--from outside, no less!--and decide a priori just what a universe must be like? The user of tensors begins with a humble attitude. The user of tensors begins, as did Riemann, ignorant of the universe--and aware of his or her ignorance. The user of tensors is obliged to calculate the coordinate system only after arriving there and is not at all free to proclaim the coordinate system in advance. Tensors can work in the Cartesian systems of ordinary graphs; they can work in Euclid's world. But it is almost as though they were created to mediate travel in Riemann's abstract universes.
Change exists in two senses: co-variation, where changes proceed in the same direction (as when a beagle chases a jackrabbit); contra -variation, as exemplified in the two ends of a stretching rubber band. And (with tensors at least) the changes can be complex mixtures of covariance and contravariances (e. g., if the beagle gains on the jackrabbit as the quarry flags from fatigue or the rubber band offers progressively more resistance as tension increases). Tensors can attain higher rank--by simultaneously representing several variations. Packaged into one entity there can be an incredible amount of information about how things are changing. Ordinary mathematics become cumbersome beyond comprehension and eventually fail in the face of what tensors do quite naturally.
If you've seen equations for complex wave, you might be led to expect tensors to occupy several pages. But the mathematician has invented very simple expressions for tensors: subscripts denote covariance and superscript indicate contravariance.[13a] If, having applied the rules and performed the calculations, R in one place doesn't equal R in another, then the transformations aren't those of a tensor and from, Brillouin's dictum, represent local fluctuations peculiar to the coordinate system; they may have empirical but not analytical meaning. If the mathematician even bothers with such parochial factors at all, he'll call them "local constants."
Many features of holograms cannot be explained by ordinary transformations. In acoustical holograms, for instance, the sound waves in the air around the microphone don't linearly transform to all changes in the receiver or on the television screen. Tensors do. The complete construction of any hologram can be regarded as tensor transformations, the reference wave doing to the object wave what transformational rules do to make, say, Rij equal Rnm . Decoding, too, is much easier to explain with tensors than with conventional mathematics. With tensors, we can drop the double and triple talk (recall the transform of the transform), especially if we place the tensors within Riemann's continuum. The back-transform of phase codes from transform space to perceptual space becomes, simply, the shift (or parallel displacement) of the same relative values from a spatial to a temporal coordinate of the same continuum.
***
We imagined mind as a version of Riemann's theoretical world, as a continuous universe of phase codes. Now we add the concept of the tensor to the picture: Tensors represent phase relationships that will transform messages, independent of any coordinates within the universe. Indeed, phase relationships, as tensors, will define the coordinates--the perception, the memory, the whatever.[13b]
***
I admit that a universe constructed from Riemann's guidelines is an exceedingly abstract entity. Diagrams, because of their Euclidean features, can undermine the very abstractions they seek to depict. But, as we did with perceptual and transform space, let's let our imaginations operate in a Euclidean world and, with reason, cautiously proceeding step by step, let's try to think our way to a higher level of intuitive understanding. Ready!
***
Imagine two points, A and B in our Euclidean world, 180 degrees apart on a circle. Let's begin a clockwise journey on a circlar course. When we arrive at 180 degrees, instead of continuing on around to 360 degrees,let's extend our journey, now counter-clockwise--to maintain our forward motion--into another circularly directed dimension, eventually arriving back at the 180 degree mark and continuing on our way to the origin; we form a figure 8. (Note that the two levels share one point -- at B.)
Notice that we "define" our universe by how we travel on it. On a curve, we of course, move continuously over all points. When we get to the 180 degree point we have to travel onto the second or lower dimension if it is there. If we don't, and elect not to count that second dimension, it may as well be "what ain't." But if the dimensions join, then a complete cycle on it is very different from an excursion around a single dimension. Notice on the 8, we must execute two 360-degree cycles to make it back to our origin. The point is that while curvature is our elemental rule, and while the relative values remain unchanged, an increase in dimensions fundamentally alters the nature of the system.
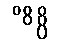 Suppose now that we add another dimension at the bottom of the lower circle
to produce a snowman. Again
our basic rules can hold up, and again relative values can transform unchanged, but,
again, the course and nature of our journey is profoundly altered beyond what
we'd experienced in one or two dimensions. For although we have a single curved
genus of figures, each universe becomes a new species.
Suppose now that we add another dimension at the bottom of the lower circle
to produce a snowman. Again
our basic rules can hold up, and again relative values can transform unchanged, but,
again, the course and nature of our journey is profoundly altered beyond what
we'd experienced in one or two dimensions. For although we have a single curved
genus of figures, each universe becomes a new species.
We could have grown additional dimensions off virtually any point on our original curve. And the sizes might vary greatly. Nor are we really compelled to remain on a flat surface. Our system might have budded like warts. And we can vary the sizes of any added dimensions. Or if we work in the abstract (as Riemann did) we can make a many-dimensional "figure" of enormous complexity. The point is that we can evolve incredible variety from a very simple rule (curvature).
***
Now let's connect hologramic theory to our discussion in this chapter.
***
If you're still struggling, don't feel bad. Instead, consider hologramic mind as analogous to operations of a pocket calculator. The buttons, display, battery and circuits--counterparts of the brain--can produce the result, say, of taking the square root of 9. The calculator and its components are very much a part of the real world. But the operations--the energy relationships within it belong to the ideal world. Of all the possible coordinates that can exist in an ideal world, one coincides with experience.
***
Believe me, I appreciate the demands Riemann's ideas can place on you, reader, especially at the outset. Therefore, allow me to offer another metaphor of hologramic mind.
Imagine a system whose rules apparently violate Riemann's curvature, a system
that seems to be governed by straight lines, sharp corners and apparent
discontinuities everywhere. What could epitomize this better than a checkerboard. Let's make that a giant red-black checkerboard.
Now imagine that one arbitrarily chosen square is
subdivided into smaller red-black checkerboard squares. Randomly select one of the
latter sub-squares and repeat the sub-squaring operation; do it again...and then
again. Appreciate that "checkerboardness" repeats itself again and again, at every level. The various
levels can be thought of as the equivalents of dimensions within our curved
continuum. We can subdivide any square as many times as we please. Because we can
pick any square for further sub-squaring--and subdivide as often as we wish--we can make any sub-checkerboards, --or sub-sub-checkerboards--carry vastly
different specific checkerboard patterns.
Okay, to complete our metaphor of hologramic mind, all we have to do is say that our red-black sets, subsets, sub-subset represent spectra of phase variations at different levels.
Now that we've created imagery, let's get rid of the checkerboard metaphor. But let's reason it out of the picture, instead of issuing a fiat.
We said that the red and black squares are infinitely divisible. Assume that we subdivide until we approach the size of a single point (as we did with the hypotenuse and our pearly e 's). If the system is infinitely divisible, then there ought to be a single unreachable point-sized square at infinity. If there are really two separate squares down there, then our system is not infinitely divisible; and if it's not infinitely divisible, where did we get the license to divide it at all? Thus we must place a single indivisible square at infinity so that we can keep on subdividing to create our metaphor. But what color is the infinite and indivisible square? Red or black? The answer is both red and black. At infinity our apparently discontinuous system becomes continuous: red and black squares superimpose and, as in Riemann's universe, the one becomes part of the other. A hidden continuity underlies the true nature of the continously repetitive pattern, and it is the reason we can systematically deal with the pattern at all. Our checkerboard metaphor of hologramic mind turns out to be a disguised version of Riemann's universe. It is, therefore, an analog not a metaphor.
***
Now let's use our general theory to answer a few questions.
How do we really account for the results of shufflebrain experiments? How could Buster's fish codes blend in smoothly with his own? How was it that Punky's salamander medulla could receive the tadpole message from the frog part of his brain? The same questions exist for "looking up." Why weren't all my experiments like pounding a square peg in a round hole? Continuity had to exist. And phase transformations had to define the coordinate system, rather than the other way around.
Consider another question, now that I've mentioned salamanders and mixing species. How can we explain the similarities and differences between them and us? Hologramic mind, constructed as a version of Riemann's universe, supplies the answer in two words: curvature and dimension. We share with all living creatures the rule of curvature, but we and they are vastly different universes by virtue of dimension. (I will return to dimension in the next chapter when discussion the cerebral cortex.)
And how can we sum together phase codes of learned and instinctive origins, if fundamentally different abstract rules govern, say, a reflex kick of a leg and a 6/8-time tarantella? We'd move like jack-jointed robots if our inner universe were a series of bolted-together but discontinuous parts. How could we condition a reflect if we couldn't smoothly blend the new information with what's already there?
Speaking of robots, we are different from the digital computer in more than the obvious ways. The computer's mind is a creature of the linear, Euclidean world of its origin. It was invented to be just that. Its memory reduces to discrete bits. A bit is a choice (usually binary)--a clean, crisp, clear, no-nonesense yes-no, on-off, either-or, black-white (or red-black) choice. And it is efficient. A computer's memories are clean, crisp, clear, linear arrays of efficient choices. By definition! By design!
By contrast, the hologramic mind is not linear; not either-or; not efficient. Hologramic mind acts flat and Euclidean and imitates the computer only when the items of discrete, discontinuous data are few. We're quickly swamped when we try to remember or manipulate an array of, say,100 individual digits, a simple task for the computer. Yet ask the digital computer to distinguish between your face and a dozen randomly sampled faces--with and without eyeglasses, lipstick and mustaches, and from various angles and distances--and it fails. Brains and computers operate on fundamentally different principles, and they mimic each other only when the task is trivial.
***
Now consider the problem that arises in perceptual vis-à-vis physical time and space. People, the author included, have reported dreaming ten-year scenes within the span of a few minutes. The reverse is probably more common: a horror lived during a second of physical time can protract into a very long perceptual interval. To the scuba diver who runs out of air, a few minutes hardly seem like a few. And time compresses during a race to the airport when we're just a few of those minutes behind schedule.
Space can do some wacky things, too. A character in a Neil Simon play tells how, during a bout of depression, he couldn't cross the street because the other side was too far away.[14]
What do we do about subjective phenomena, anyway? Discount them from Nature because they're "only in the mind."
In Fourier (and kindred) transforms, the time-dependent features of relative phase became space-dependent. But the relationships in transform space obey what time-dependent ones do in perceptual space: the axes don't contract and expand. Tensors, on the other hand, aren't constrained by presumptions about coordinate axes. In the curved continuum, time-dependent ratios may turn up on an elastic axis. And because the hologramic universe is a continuum, we lose the distinction between perceptual and some other kind of space; or we may have the conscious impression that time is expanding or that distances will not close. Yes, it's ideal, subjective, illusory. Subjective time and space are informational transforms of what the clock gauges and the meter stick plots. The constraints on the clock and meter stick are physical. Constraints on the transformations of the mind are ideal. But both belong to Nature.
***
But hologramic theory suffers a major deficit, and we will have to correct it. Our construct is too perfect, too ball-bearing smooth, too devoid of errors, for twig missing from the nest or the freckles on a face. We can't see ourselves in the picture. We must account in our theory for what doesn't transform, what won't remain invariant in all other coordinates. Our pictures requires precisely what the pure theoretician goes to great pains to get out of the way--parochial conditions, particular features, local constants! Physiologist E. Roy John, recall (from chapter 2) identifies local constants as noise. I believe we must also put amplitude among our local constants. (Experimentation may uncover others.)
Local constants make perception distinct from recollection of the original percept. They make a kiss different from a reminiscence of it. They put subtle but critical shades of difference on the spoken versus the written word. (Notice some time when you're listening to a correspondent deliver the news from a script the subtle change that occurs when he or she shifts to the ad lib to answering of questions from the anchor person.) Local constants become essential when the general becomes the particular; when the ideal, abstract, informational hologramic mind transduces into experiences; where theory stops and experiments take over.
Because they are strictly parochial, the local constants necessarily vary with each individual. And the more dimensions a mind uses, the greater the impact of local constants on the collective behavior of the species. Hologramic theory, thus, is a self-limiting theory.
We should not underestimate a theory's implications merely because the theory limits itself (as any scientific theory eventually must). A little humility can actually go a long way, as Riemann found. The latter is true of hologramic theory. Let me illustrate what I'm driving at by calling upon the checkerboard metaphor.
To the red squares, let's assign relative phase tensors and everything else we explicitly use in hologramc theory. To the black squares, let's assign our local constants--which we can't directly treat from hologramic theory. To guarantee that the theory continues to restrict itself, let's maintain the rule that we cannot enter a black square from a red square, and vice verse. With this rule in mind, let's subdivide squares again and again, as we did before, and let's pose the same question: is the infinite square red or black? Just as before, it has to be both red and black. We still can't enter the infinite square. But this time, it's not the math book that bars us from infinity. It's our own rule. Both black and red exist at infinity. If one up from infinity is red, and we're there, we can't enter the next set (infinity) because it contains black and is off limits. (Note that how red and black got to infinity in the first place isn't our affair. We didn't put infinity there, since we couldn't reach it in the first place.) Thus the infinite square precludes hologramic theory (red) from using local constants (black) and vice versa.
When we're on the red square, the "mechanism" that inhibits our movement into the infinite square is the corresponding black square, also a step up from infinity. Ironically, the very self-limiting nature of hologramic theory establishes the existence--the Existenz--of the domain with our local constants.[15]
In formal terms, the incompleteness of hologramic theory makes local constants an existential necessity. The term existential refers to existence.
The very incompleteness of the theory allows us to use it to resolve the mind-brain conundrum. Hologramic theory deals explicitly with mind. Yet it can do so only because it implicates local constants. And local constants exist in the brain. In other words, hologramic theory must work within a mind-brain system. A corollary of the last statement is that the source of the mind-brain conundrum was the fallacy, inherent in holism and structuralism alike, that a unipolar view can let us comprehend the mind-brain cosmos. Once we remove this fallacy and allow mind and brain to get back together again, the conundrum vanishes. Mind endows brain with the abstract universe in which to contain the realm of thought. But brain, in turn, gives life to the mind.
We must reach outside hologramic theory to give perspective to our conclusions. And I know of no system of thought more perfectly suited to our needs than Hegelian dialectics, in which a thesis merge with its antithesis to create a synthesis.
What is the mind-brain synthesis? You and I are! They are! It is general and ideal, as we all are. And it is particular and real, as we are too.
Internet contact:pietsch@indiana.edu